Точка T-середина ребра cc1 куба abcda1b1c1d1. Постройте сечение куба плоскостью , которая проходит через точку Т и параллельна плоскости bc1d. Вычислите площадь поверхности куба , если площадь полученного сечения равна 4V3(V-корень)
Ответы
Решение дано Пользователем 21sadtylers Отличник, исправлена опечатка.
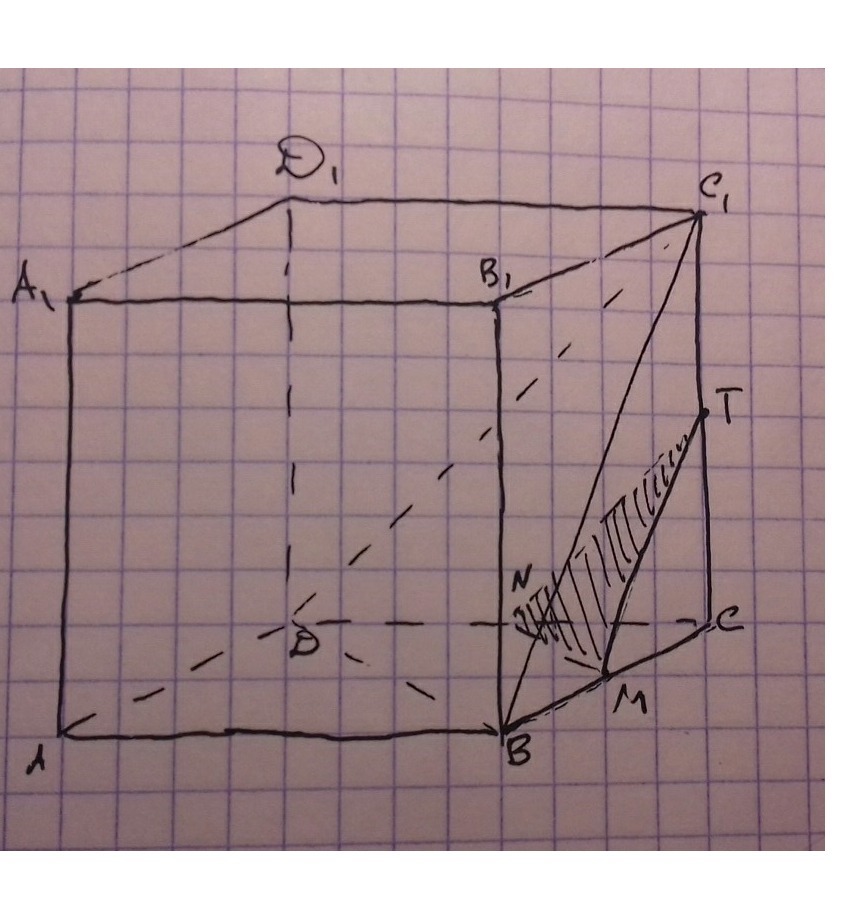
Для начала изобразим плоскость bc1d. Это совсем несложно – каждая пара точек лежит в одной из граней куба, поэтому просто соединим их. Далее проведём ТМ||С1В, ТN||C1D, соединим M и N – получим искомое сечение.
BC1D – равносторонний, т.к. каждая сторона является диагональю одинаковых квадратов. Все стороны TMN вдвое меньше сторон BC1D – это видно в треугольниках, для которых стороны TMN являются средними линиями. Получается, TMN тоже равносторонний. Найдем его сторону.
Площадь правильного треугольника можно найти по формуле S=a²√3/4.
Выразим а=√(4S/√3)=√(4*4√3/√3)=4.
Посмотрим на треугольник СМТ: он прямоугольный и равнобедренный, можем найти его стороны по теореме Пифагора:
ТМ² = 2СМ²
СМ = √(ТМ²/2) = √(4²/2) = √8 = 2√2
найдем ребро куба: 2*2√2 = 4√2
ну и площадь поверхности:
S = 6a² = 6*(4√2)² = 6*32 = 192 кв. ед.