Предмет: Алгебра,
автор: Anastasiya5620
решите логарифмическое неравенство
Приложения:
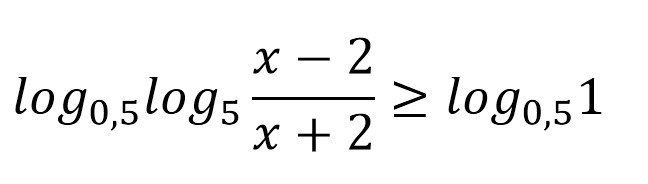
Ответы
Автор ответа:
0
это убывающая функция т.к. 0<0,5<1 , поэтому знак неравенства поменяется. Не забываем, что аргумент логарифма должен быть положительным.
это возрастающая функция т.к. 5>1, поэтому знак неравенства сохранится.
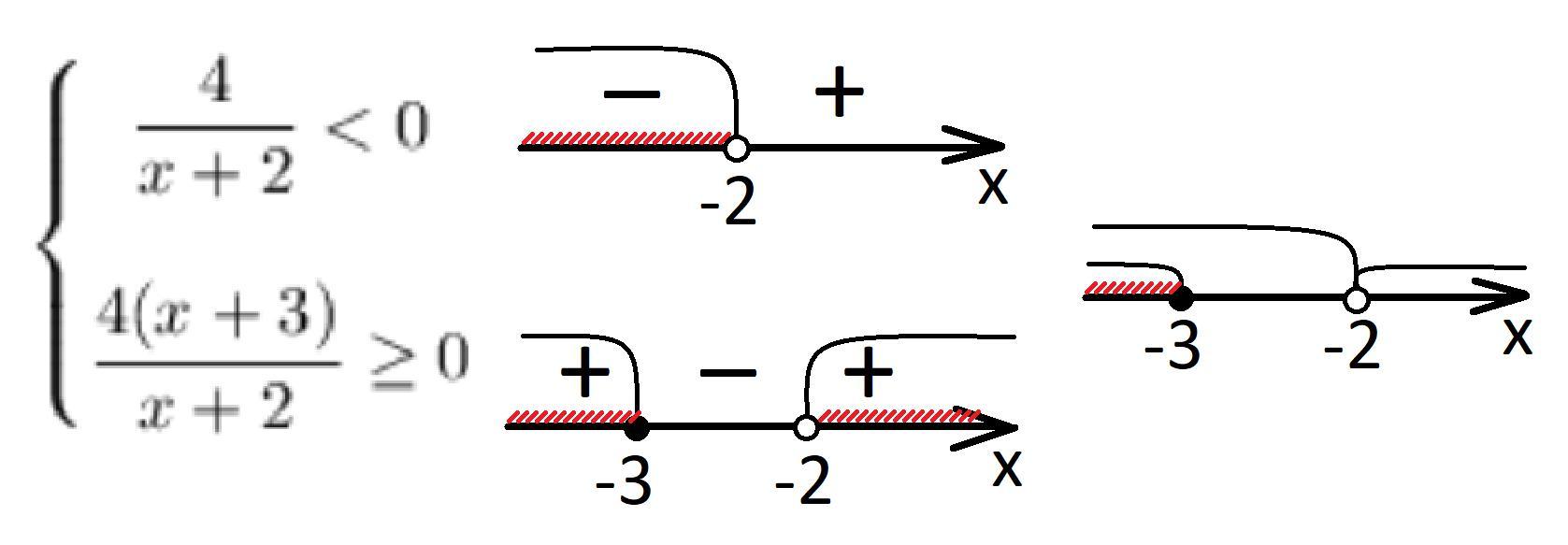
Остальное решение смотри на фото.
Ответ: x∈(-∞ ; -3].
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: colsdldl
Предмет: Математика,
автор: Dron129
Предмет: Другие предметы,
автор: APma2rim
Предмет: География,
автор: dianameleshkev
Предмет: Алгебра,
автор: апррош