Question

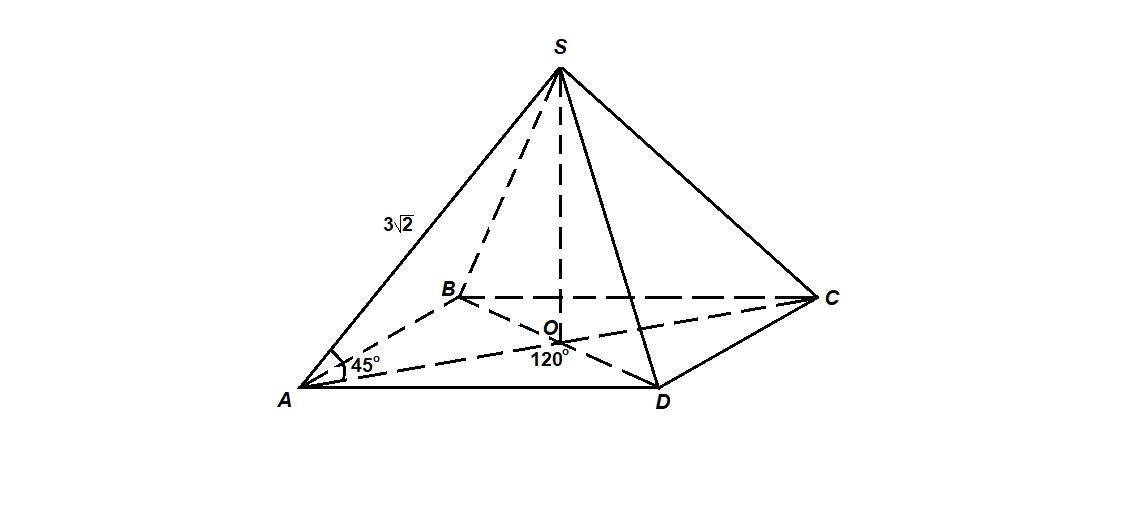
Основание пирамиды-прямоугольник с углом между диагоналями 120 градусов. Все боковые ребра пирамиды равны 3(корень из)2 см и наклонены к плоскости основания под углом 45 градусов. Найдите V пирамиды.

Answer 1

Ответ:   9√3 см³

Объяснение:

Если боковые ребра пирамиды равны, то высота проецируется в центр окружности, описанной около основания. В прямоугольнике - это точка пересечения диагоналей.

Итак, SO - высота пирамиды, тогда ОА - проекция бокового ребра SA на плоскость основания, следовательно ∠SAO = 45° - угол наклона бокового ребра к плоскости основания.

ΔSOA прямоугольный, острый угол равен 45°, значит он равнобедренный.

$AO=SO=frac{SA}{sqrt{2}}=3$  см  (так как гипотенуза равнобедренного прямоугольного треугольника с катетом а равна а√2 )

Диагонали прямоугольника равны и точкой пересечения делятся пополам:

BD = АС = 2АО = 6 см

Sabcd = 1/2 AC · BD · sin∠AOD

Sabcd = 1/2 · 6 · 6 · √3/2 = 9√3 см²

V = 1/3 Sabcd · SO = 1/3 · 9√3 · 3 = 9√3 см³