Question

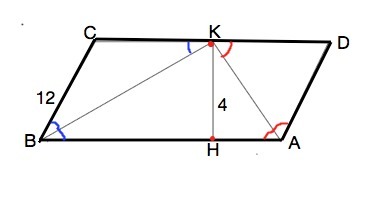
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K лежащей на стороне CD. Найдите площадь параллелограмма, если BC = 12 см, а расстояние от точки K до стороны AB равно 4 см

Answer 1

∠ КВС=∠КВА (ВК - биссектриса и делит ∠СВА пополам). 

∠СКВ=∠КВА ( накрестлежащие при СD ║ ВА и секущей ВК). 

∠СКВ=∠СВК, след. ∆ ВСК - равнобедренный и СК=ВС=12. 

∠КАВ=∠КАD ( АК - биссектриса). 

∠DКА=∠КАВ ( накрестлежащие).⇒ ∆ КDА - равнобедренный. КD=AD 

В параллелограмме противоположные стороны равны. 

След. AD=ВС=12 Сторона СD=12+12=24. Стонона АВ=CD=24 

Расстояние между параллельными прямыми измеряется перпендикулярным к ним отрезком. КН - перпендикулярен АВ.  

КН - высота АВСD.

Площадь параллелограмма находят произведением его высоты на сторону, к которой она проведена. 

S=КН•AB=4•24=96 см²