Предмет: Геометрия,
автор: Taras155
Помогите пожалуйста решить задачу по геометрии с обьяснениями
За помощь даю 40 баллов!
Помогите пожалуйста решить задачу, очень нужно
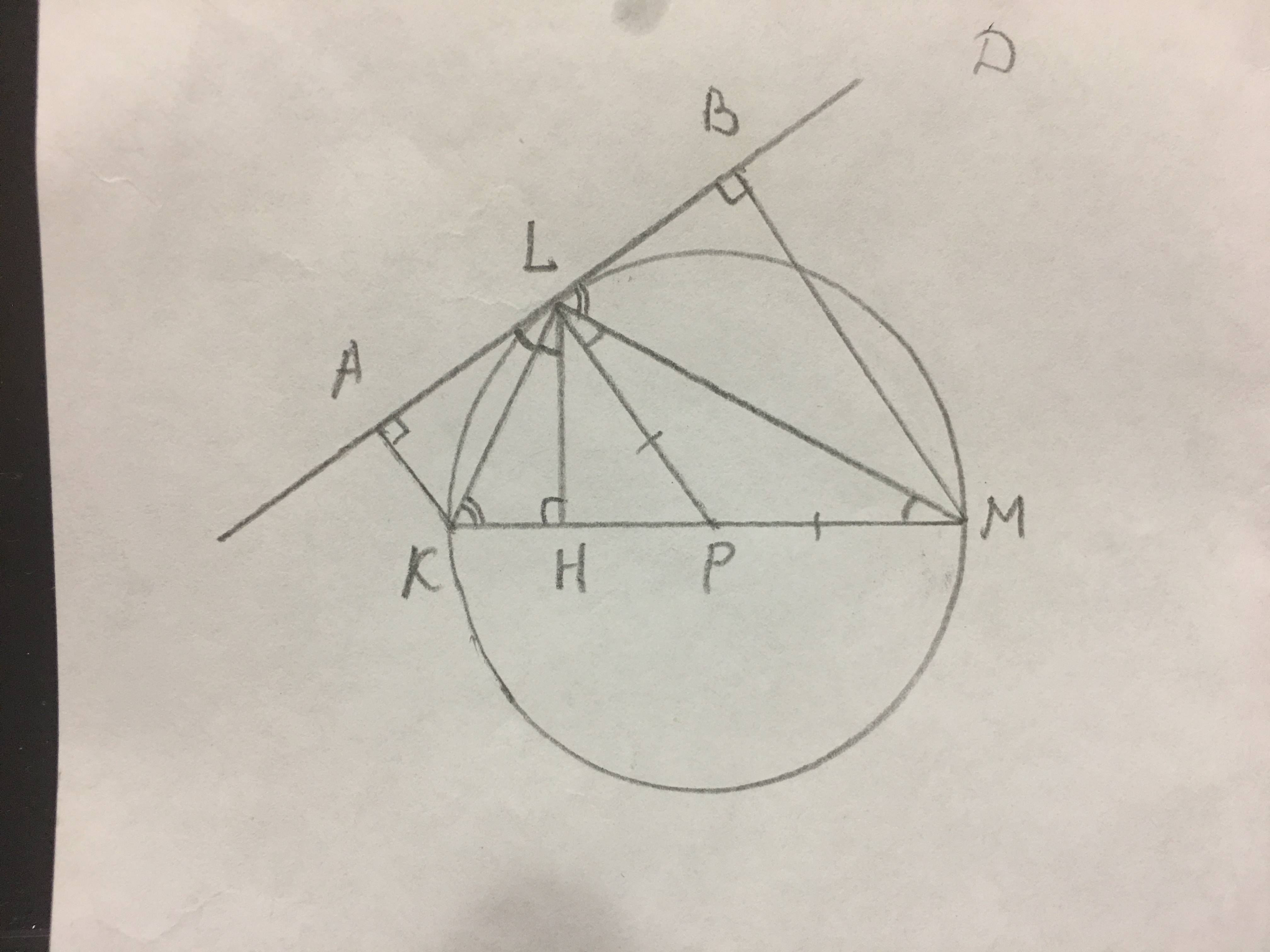
Отрезок KM является диаметром окружности, а точка L принадлежит окружности. Расстояния от точек K и M к касательной, проведенной в точке L, равни 4 и 20 см соотвественно. Найдите радиус окружности
Ответы
Автор ответа:
0
Треугольник LKM прямоугольный т.к. КМ диаметр окружности.
КА=4 см, МВ=20 см.
КМ=?
Проведём высоту LН и медиану LP. LP - радиус. LP⊥AB.
Тр-ник LРМ равнобедренный, значит ∠MLP=∠LMP.
∠MLB=∠РLB-∠MLP=90-∠LMK=∠LKM.
Тр-ки LMH и LMВ равны по углам и общей гипотенузе, значит МН=МВ=20 см.
Треугольники LKM и LKH подобны, значит ∠LMK=∠KLH.
∠HLP=∠KLM-∠KLH-∠MLP=90-2∠LMK.
∠ALK=∠ALP-∠HLP-KLH=90-(90-2∠LKM)-∠LKM=∠LKM.
Треугольники ALK и KLH равны по углам и общей гипотенузе, значит КН=АК=4 см.
Итак, КМ=КН+МН=4+20=24 см - это ответ.
КА=4 см, МВ=20 см.
КМ=?
Проведём высоту LН и медиану LP. LP - радиус. LP⊥AB.
Тр-ник LРМ равнобедренный, значит ∠MLP=∠LMP.
∠MLB=∠РLB-∠MLP=90-∠LMK=∠LKM.
Тр-ки LMH и LMВ равны по углам и общей гипотенузе, значит МН=МВ=20 см.
Треугольники LKM и LKH подобны, значит ∠LMK=∠KLH.
∠HLP=∠KLM-∠KLH-∠MLP=90-2∠LMK.
∠ALK=∠ALP-∠HLP-KLH=90-(90-2∠LKM)-∠LKM=∠LKM.
Треугольники ALK и KLH равны по углам и общей гипотенузе, значит КН=АК=4 см.
Итак, КМ=КН+МН=4+20=24 см - это ответ.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: makarbobrov031
Предмет: Английский язык,
автор: andreyjon
Предмет: Химия,
автор: v240
Предмет: Математика,
автор: эльза9999
Предмет: Физика,
автор: умар141