Предмет: Алгебра,
автор: nis31
Помогите решить две системы(желательно с объяснением)
Приложения:
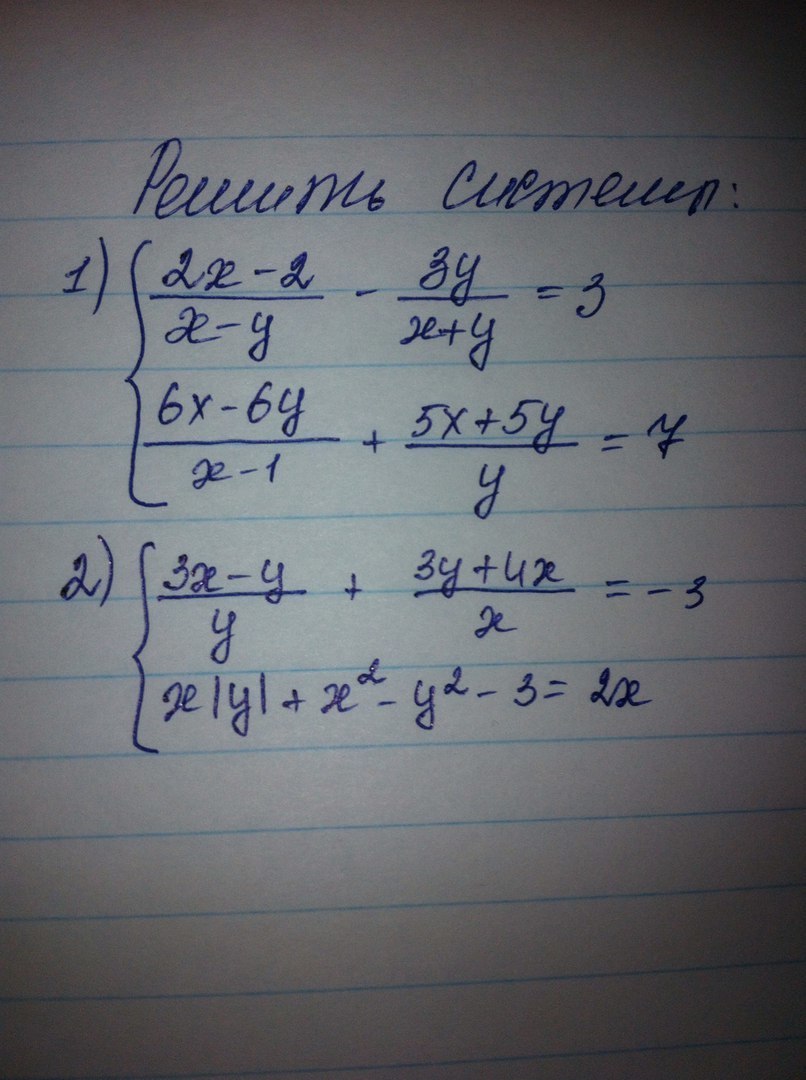
Ответы
Автор ответа:
0
1) Перепишем так


Замена ;
; 
{ 2a - 3b = 3
{ 6/a + 5/b = 7
Из 1 уравнения b = (2a - 3)/3; подставляем во 2 уравнение
6/a + 5*3/(2a - 3) = 7
6(2a - 3) + 15a = 7a(2a - 3)
12a - 36 + 15a = 14a^2 - 21a
14a^2 - 21a - 27a + 36 = 0
14a^2 - 48a + 36 = 0
7a^2 - 24a + 18 = 0
D/4 = 12^2 - 7*18 = 144 - 126 = 18 = (3√2)^2
a1 = (12 - 3√2)/7; b1 = (2a - 3)/3 = (3 - 6√2)/21
a2 = (12 + 3√2)/7; b2 = (2a - 3)/3 = (3 + 6√2)/21
Обратная замена
1)


Перейдем от дробей к целым числам
{ 7(x - 1) = (12 - 3√2)(x - y)
{ 7y = (1 - 2√2)(x + y)
Раскроем скобки
{ 7x - 7 = (12 - 3√2)*x - (12 - 3√2)*y
{ 7y = (1 - 2√2)*x + (1 - 2√2)*y
Переносим переменные отдельно, числа отдельно
{ (5 - 3√2)*x - (12 - 3√2)*y = -7
{ (1 - 2√2)*x + (-6 - 2√2)*y = 0
Умножаем 1 уравнение на (-6 - 2√2), 2 уравнение на (12 - 3√2)
{ (5 - 3√2)(-6 - 2√2)*x - (12 - 3√2)(-6 - 2√2)*y = -7(-6 - 2√2)
{ (1 - 2√2)(12 - 3√2)*x + (12 - 3√2)(-6 - 2√2)*y = 0
Складываем уравнения
x*[ (5 - 3√2)(-6 - 2√2) + (1 - 2√2)(12 - 3√2) ] = 7(6 + 2√2)
Отсюда находим x1 и y1.
2)


Перейдем от дробей к целым числам
{ 7(x - 1) = (12 + 3√2)(x - y)
{ 7y = (1 + 2√2)(x + y)
Раскроем скобки
{ 7x - 7 = (12 + 3√2)*x - (12 + 3√2)*y
{ 7y = (1 + 2√2)*x + (1 + 2√2)*y
Переносим переменные отдельно, числа отдельно
{ (5 + 3√2)*x - (12 + 3√2)*y = -7
{ (1 + 2√2)*x + (-6 + 2√2)*y = 0
Умножаем 1 уравнение на (-6 + 2√2), 2 уравнение на (12 + 3√2)
{ (5 + 3√2)(-6 + 2√2)*x - (12 + 3√2)(-6 + 2√2)*y = -7(-6 + 2√2)
{ (1 + 2√2)(12 + 3√2)*x + (12 + 3√2)(-6 + 2√2)*y = 0
Складываем уравнения
x*[ (5 + 3√2)(-6 + 2√2) + (1 + 2√2)(12 + 3√2) ] = 7(6 - 2√2)
Отсюда находим x2 и y2.
Замена
{ 2a - 3b = 3
{ 6/a + 5/b = 7
Из 1 уравнения b = (2a - 3)/3; подставляем во 2 уравнение
6/a + 5*3/(2a - 3) = 7
6(2a - 3) + 15a = 7a(2a - 3)
12a - 36 + 15a = 14a^2 - 21a
14a^2 - 21a - 27a + 36 = 0
14a^2 - 48a + 36 = 0
7a^2 - 24a + 18 = 0
D/4 = 12^2 - 7*18 = 144 - 126 = 18 = (3√2)^2
a1 = (12 - 3√2)/7; b1 = (2a - 3)/3 = (3 - 6√2)/21
a2 = (12 + 3√2)/7; b2 = (2a - 3)/3 = (3 + 6√2)/21
Обратная замена
1)
Перейдем от дробей к целым числам
{ 7(x - 1) = (12 - 3√2)(x - y)
{ 7y = (1 - 2√2)(x + y)
Раскроем скобки
{ 7x - 7 = (12 - 3√2)*x - (12 - 3√2)*y
{ 7y = (1 - 2√2)*x + (1 - 2√2)*y
Переносим переменные отдельно, числа отдельно
{ (5 - 3√2)*x - (12 - 3√2)*y = -7
{ (1 - 2√2)*x + (-6 - 2√2)*y = 0
Умножаем 1 уравнение на (-6 - 2√2), 2 уравнение на (12 - 3√2)
{ (5 - 3√2)(-6 - 2√2)*x - (12 - 3√2)(-6 - 2√2)*y = -7(-6 - 2√2)
{ (1 - 2√2)(12 - 3√2)*x + (12 - 3√2)(-6 - 2√2)*y = 0
Складываем уравнения
x*[ (5 - 3√2)(-6 - 2√2) + (1 - 2√2)(12 - 3√2) ] = 7(6 + 2√2)
Отсюда находим x1 и y1.
2)
Перейдем от дробей к целым числам
{ 7(x - 1) = (12 + 3√2)(x - y)
{ 7y = (1 + 2√2)(x + y)
Раскроем скобки
{ 7x - 7 = (12 + 3√2)*x - (12 + 3√2)*y
{ 7y = (1 + 2√2)*x + (1 + 2√2)*y
Переносим переменные отдельно, числа отдельно
{ (5 + 3√2)*x - (12 + 3√2)*y = -7
{ (1 + 2√2)*x + (-6 + 2√2)*y = 0
Умножаем 1 уравнение на (-6 + 2√2), 2 уравнение на (12 + 3√2)
{ (5 + 3√2)(-6 + 2√2)*x - (12 + 3√2)(-6 + 2√2)*y = -7(-6 + 2√2)
{ (1 + 2√2)(12 + 3√2)*x + (12 + 3√2)(-6 + 2√2)*y = 0
Складываем уравнения
x*[ (5 + 3√2)(-6 + 2√2) + (1 + 2√2)(12 + 3√2) ] = 7(6 - 2√2)
Отсюда находим x2 и y2.
Автор ответа:
0
Да, поэтому я даже с первой не начинал. Идея легкая- вычислений дофига
Похожие вопросы
Предмет: Биология,
автор: luchkinslava
Предмет: Биология,
автор: piskovecdanil
Предмет: Геометрия,
автор: Jykitro
Предмет: Литература,
автор: yanyanov
Предмет: История,
автор: рашидова