Question

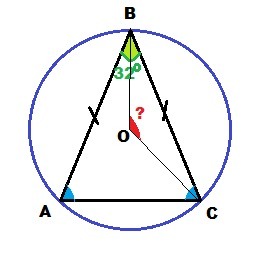
окружность с центром в точке О описана окало равнобедренного треугольника АВС , в котором АВ =ВС и <АВС=32°. найдите угол ВОС . ответ дайте в градусах

Answer 1

ΔABC - равнобедренный, ∠ABC = 32°;  AB = BC   ⇒
∠BAC = ∠BCA = (180° - ∠ABC) /2 = (180° - 32°) /2 = 74°

∠BAC - вписанный угол, градусная мера вписанного угла равна половине дуги, на которую этот угол опирается.
∠BAC = ∪ BC/2  ⇒   ∪ BC = 2∠BAC = 2*74° = 148°

∠BOC - центральный угол, градусная мера центрального угла равна дуге, на которую этот угол опирается.  ⇒
∠BOC = ∪ BC = 148°

Ответ: ∠BOC = 148°