Question

Помогите, плиз!
Доведіть що коли в трапеції діагоналі перпендикулярні, то сума квадратів діагоналей дорівнює квадрату суми основ.(Укр.)
Докажите что когда в трапеции диагонали перпендикулярны, то сумма квадратов диагоналей равна квадрату суммы оснований.(Русский)

Answer 1

ABCD-трапеция,AC и BD диагонали,AC_|_BD,O-точка пересечения
ΔBOC∞ΔAOD по 2 равным накрест лежащим углам.
Тогда BO/OD=CO/OA=k-коэффициент подобия
Следовательно BO=k*OD,CO=K*OA
Найдем
(BC+AD)²=(√(BO²+OC²)+√(OA²+OD²))²=√(√k²OD²+k²OA²)+√(OA²+OD²))²=
=(√(OA²+OD²))²*(k+1)²=(OA²+OD²)*(k+1)²
Найдем
AC²+BD²=(BO+OD)²+(OC+OA)²=(kOD+OD)²+(kOA+OA)²=
=OD²(k+1)²+OA²(k+1)²=(OD²+OA²)*(k+1)²
Получили
(BC+AD)²=AC²+BD² (если равны правые части,то равны и левые)

71fd0d975e263785f36a47610be62d01.docx

Answer 2

Нарисуй рисунок плиз

Answer 3

А тут ничего не понятно(

Answer 4

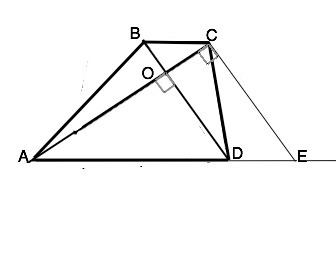
Проведем прямую  из вершины С параллельно диагонали BD до пересечения с продолжением АD в точке Е. 

∠АСЕ =∠АОD как соответственные при пересечении параллельных ВD и СЕ и секущей АС.  ⇒ ∆ АСЕ - прямоугольный.

В четырехугольнике ВСЕD противоположные стороны параллельны. ВСЕD -  параллелограмм и ВС=DE.  ⇒ 

АЕ=АD+DE. По т.Пифагора квадрат гипотенузы АЕ равен сумме квадратов катетов АС и СЕ. А так как АЕ равна сумме оснований, а СЕ=BD, то 

АС²+ВD²=(AD+BC)², что и требовалось доказать.

Answer 5

Тут легче и понятно