Question

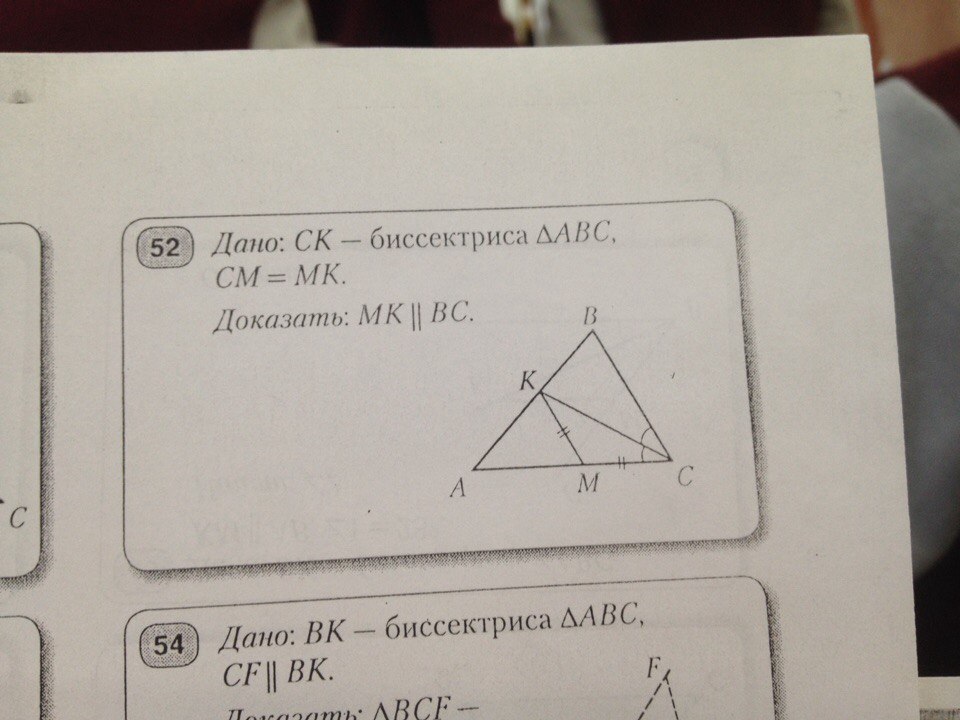
задача 1)дано: CK-биссектриса треугольника ABC; CM=MK; Доказать MK//BC
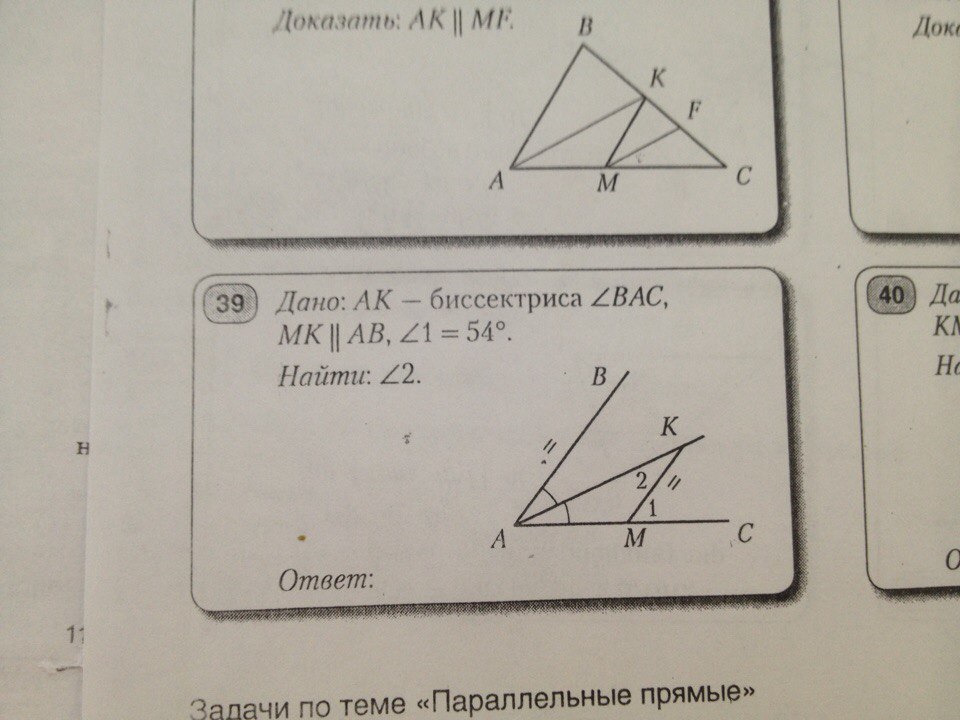
задача 2)ak-биссектриса угла bac, mk//ab, угол 1=54*, найти угол 2

Answer 1

Ответ: 2)  27°

Объяснение:

1)

∠МСК = ∠МКС как углы при основании равнобедренного треугольника МКС,

∠МСК = ∠ВСК, так как СК биссектриса ΔАСВ,  ⇒

∠МКС = ∠ВСК, а эти углы - накрест лежащие при пересечении прямых МК и ВС секущей СК, значит

МК ║ ВС.

2)

∠ВАМ = ∠1 = 54° как соответственные при  пересечении параллельных прямых МК и АВ секущей АС.

∠ВАК = 1/2 ∠ВАМ = 1/2 · 54° = 27°, так как АК - биссектриса ∠ВАС.

∠2 = ∠ВАК = 27° как накрест лежащие при пересечении параллельных прямых МК и АВ секущей АК.