Предмет: Алгебра,
автор: ashen
Решите неравенство с логарифмами:
Приложения:
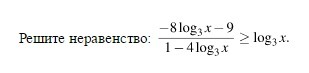
Ответы
Автор ответа:
0
Обозначим log_3 x=t;
(-8t-9)/(1-4t)≥t;
(8t+9)/(4t-1)-t≥0;
(8t+9-4t^2+t)/(4t-1)≥0;
(4t^2-9t-9)/(4t-1)≤0;
(t-3)(4t+3)/(4t-1)≤0;
t∈(-∞;-3/4]∪(1/4;3].
1 случай. log_3 x≤ - 3/4; x∈(0; 3^(-3/4)]
2 случай 1/4< log_3 x≤3; x∈(3^(1/4);27]
Ответ: (0; 3^(-3/4)]∪ (3^(1/4);27]
(-8t-9)/(1-4t)≥t;
(8t+9)/(4t-1)-t≥0;
(8t+9-4t^2+t)/(4t-1)≥0;
(4t^2-9t-9)/(4t-1)≤0;
(t-3)(4t+3)/(4t-1)≤0;
t∈(-∞;-3/4]∪(1/4;3].
1 случай. log_3 x≤ - 3/4; x∈(0; 3^(-3/4)]
2 случай 1/4< log_3 x≤3; x∈(3^(1/4);27]
Ответ: (0; 3^(-3/4)]∪ (3^(1/4);27]
Похожие вопросы
Предмет: Русский язык,
автор: Novruz12
Предмет: Математика,
автор: linkur
Предмет: Химия,
автор: viktorijakapusta16
Предмет: Математика,
автор: ящур1803
Предмет: Математика,
автор: danil1805