Предмет: Алгебра,
автор: ashen
Решите неравенство:
Приложения:
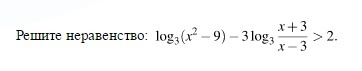
Ответы
Автор ответа:
0
ОДЗ:
---------+-------(-3)--------- - --------(3)--------+--------
///////////////////// //////////////////////
------+------(0)------ - -------(9)-------+----------
///////////////// /////////////////////
учтем ОДЗ
Ответ: (- ∞; -3) ∪ (9; + ∞)
Похожие вопросы