Question

Помогите 143 решить пжл

Answer 1

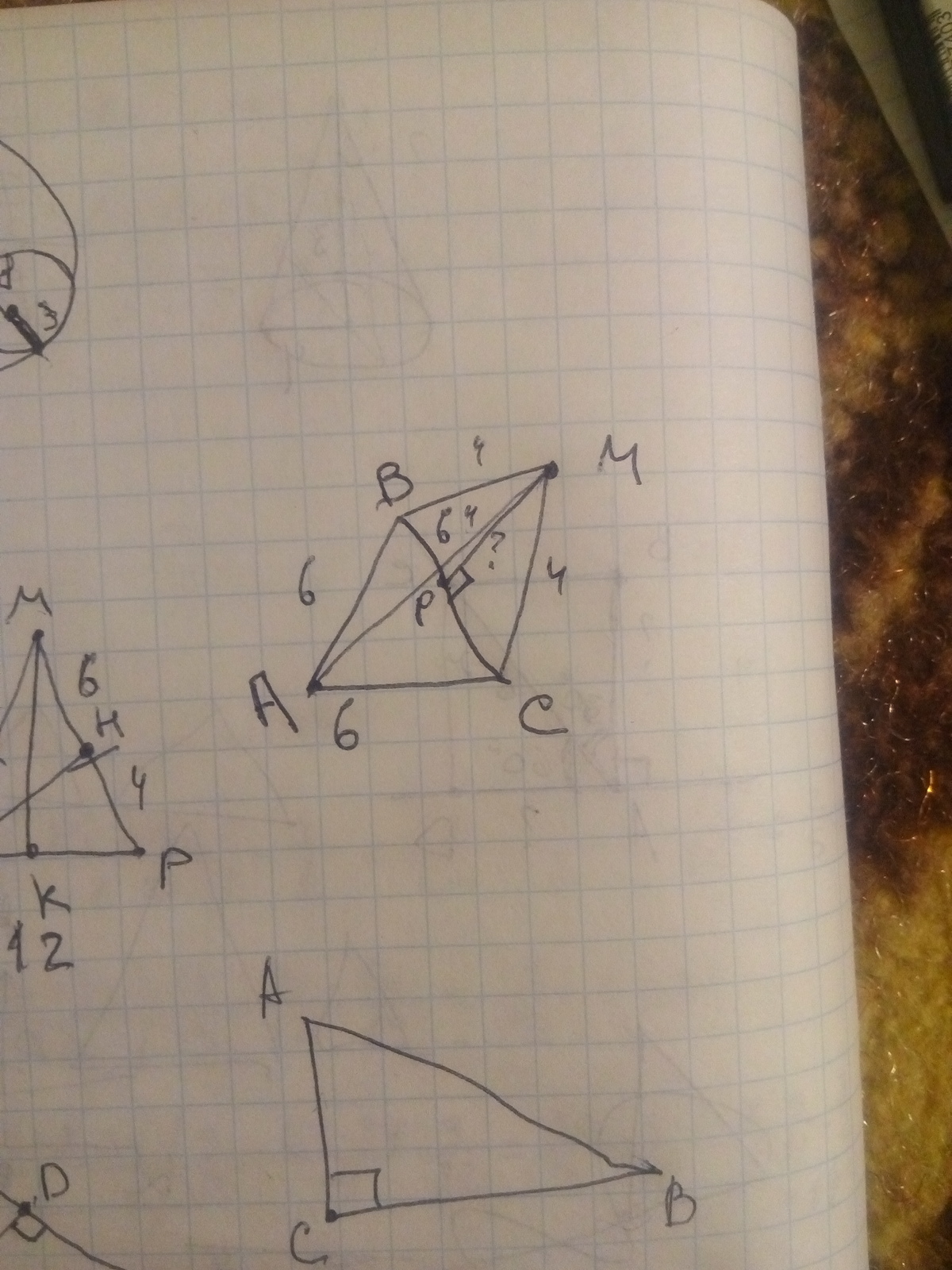
рассмотрим треугольник образованный перпендикуляром из точки М на плоскость АВС, треугольник​ МРС, угол МРС=90°, МС= 4; РС=ВС/2=6/2=3см.(МР является медианой треугольника ВМС, т.к. этот треугольник равнобедренный)
МРС- прямоугольный треугольник, так что будем считать по теореме Пифагора:
МС²=РМ²+РС², отсюда выводим нужный катет
РМ²=МС²-РС²=4²-3²=16-9=7
РМ=√7≈2.645(см)
Ответ: расстояние от точки М до плоскости АВС= РМ=√7 или 2.645 см.