Предмет: Математика,
автор: Vit4alreworiya
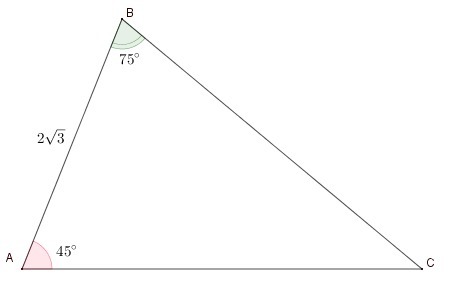
решите треугольник ABC, если угол A = 45, угол B = 75, AB = 2 корня из 3
Ответы
Автор ответа:
0
Ответ: ∠C = 60°; BC = 2√2; AC = √2 + √6.
Пошаговое объяснение:
Сумма внутренних углов треугольника равна 180°.
∠A + ∠B + ∠C = 180°
∠C = 180° - ∠A - ∠B = 180° - 45° - 75° = 60°.
По теореме синусов:
Представим 75 как сумму 45 и 30, тогда
Приложения:
Похожие вопросы
Предмет: Математика,
автор: 2634693
Предмет: Алгебра,
автор: ulakapitan584
Предмет: Английский язык,
автор: bogdanlo863
Предмет: Литература,
автор: Марьяна100000646