Предмет: Алгебра,
автор: Alex364
Вычислите площадь фигуры, ограниченной линиями: y=x^2, y=x^(-1), y=e. Ну или хотя бы какой то интеграл получится и первообразная? Спасибо!
Ответы
Автор ответа:
0
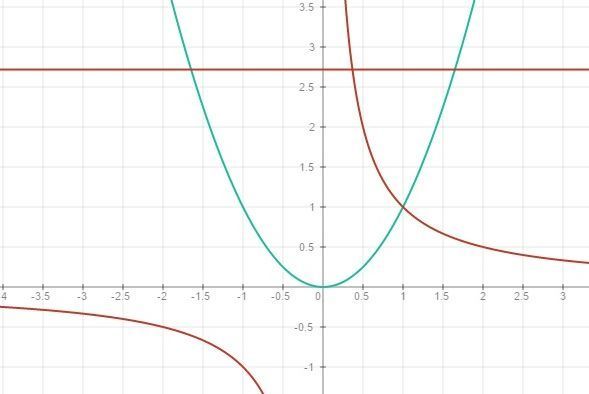
в приложенной картинке видно, что у нас 2 области - вместе они составляют площадь под линией у=е. точки пересечения горизонтали у=е и параболой у=х² х²=е x=√e x=-√e
площадь прямоугольника под у=е е*2√е
площадь под параболой ∫x²dx от -√е до +√е или в силу симметрии
удвоенному интегралу от 0 до √е
2∫х²dx=2/3*x³ 2*F(0)=0 s1=2*F(√e)=4/3*(√e)³=4/3*e√e
искомая s=2e√e-4/3e√e=2/3*e√e
площадь прямоугольника под у=е е*2√е
площадь под параболой ∫x²dx от -√е до +√е или в силу симметрии
удвоенному интегралу от 0 до √е
2∫х²dx=2/3*x³ 2*F(0)=0 s1=2*F(√e)=4/3*(√e)³=4/3*e√e
искомая s=2e√e-4/3e√e=2/3*e√e
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: edinorog9660
Предмет: Математика,
автор: kratcinna
Предмет: Геометрия,
автор: 12345675634643
Предмет: Математика,
автор: 150022