Предмет: Алгебра,
автор: rrrrtttt01
Пожалуйста помогите........................
Приложения:
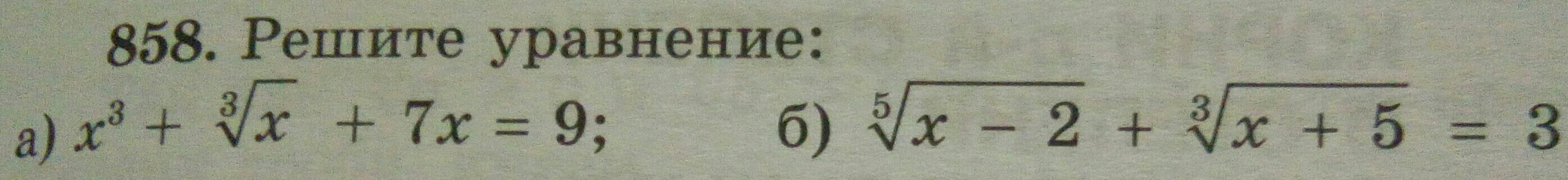
Ответы
Автор ответа:
0
Рассмотрим функцию
Легко заметить, то число 1 - корень уравнения:
Других корней уравнение не имеет.
Ответ: 1
Аналогично, функция
Других корней уравнение не имеет.
Ответ: 3
Похожие вопросы
Предмет: Математика,
автор: Artemvoo
Предмет: Английский язык,
автор: maranaz4rova
Предмет: Английский язык,
автор: maranaz4rova
Предмет: Математика,
автор: Алена555Алена
Предмет: Математика,
автор: поля95