Предмет: Алгебра,
автор: Кариночка78
Решите, пожалуйста, уравнения.
Приложения:
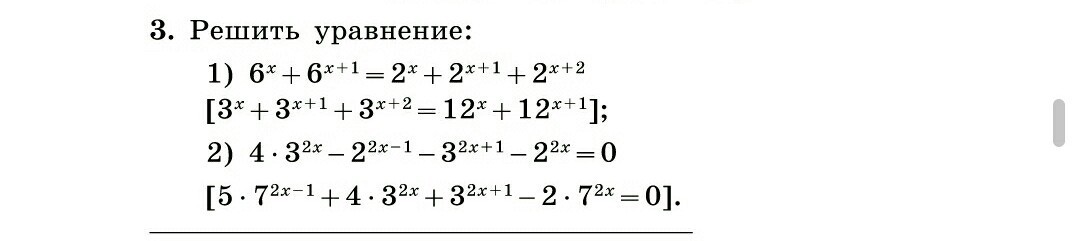
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: matom61
Предмет: Информатика,
автор: j76dy45896
Предмет: Биология,
автор: matom61
Предмет: Математика,
автор: 89034859933
Предмет: Математика,
автор: стася0107