Предмет: Алгебра,
автор: Кариночка78
Решить систему уравнений
Приложения:
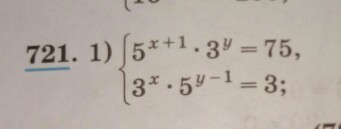
Ответы
Автор ответа:
0
Ответ: (1; 1)
Автор ответа:
0
спасибо
Похожие вопросы
Предмет: Математика,
автор: kratcinna
Предмет: Химия,
автор: nokiirina253
Предмет: Математика,
автор: kratcinna
Предмет: Математика,
автор: Мадина05
Предмет: История,
автор: Ритуля067