Question

Помогите срочно:
В прямоугольном параллелепипеде АD = 3, DС = 4, СС1 = k. Через ребро С1С и
середину АD проведена плоскость сечения. Найдите площадь сечения параллелепипеда

Answer 1

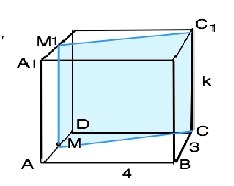
Обозначим середину АD точкой М. Соединим М и С, лежащие в плоскости АВСD. Верхняя и нижняя грани параллелепипеда параллельны, следовательно, линия С1М1 сечения параллельна линии СМ. Ребра сечения  перпендикулярны плоскости АВСD. Сечение СММ1С1- прямоугольник со сторонами СМ=C1М1 и ММ1=СС1.  

Площадь прямоугольника равна произведению его соседних сторон. S=СC1•СM.  Из прямоугольного ∆ СМD СМ=√((0,5AD)²+CD²)=√(2,25+16)=√(1825/100)=0,5√73 ⇒ S(ММ1С1С)=k•0,5√73 (ед. площади)