Предмет: Геометрия,
автор: VeryBusyPerson
Дано:
AB=BD
BE параллельно DC
Доказать:
DC пересекается AC
Приложения:
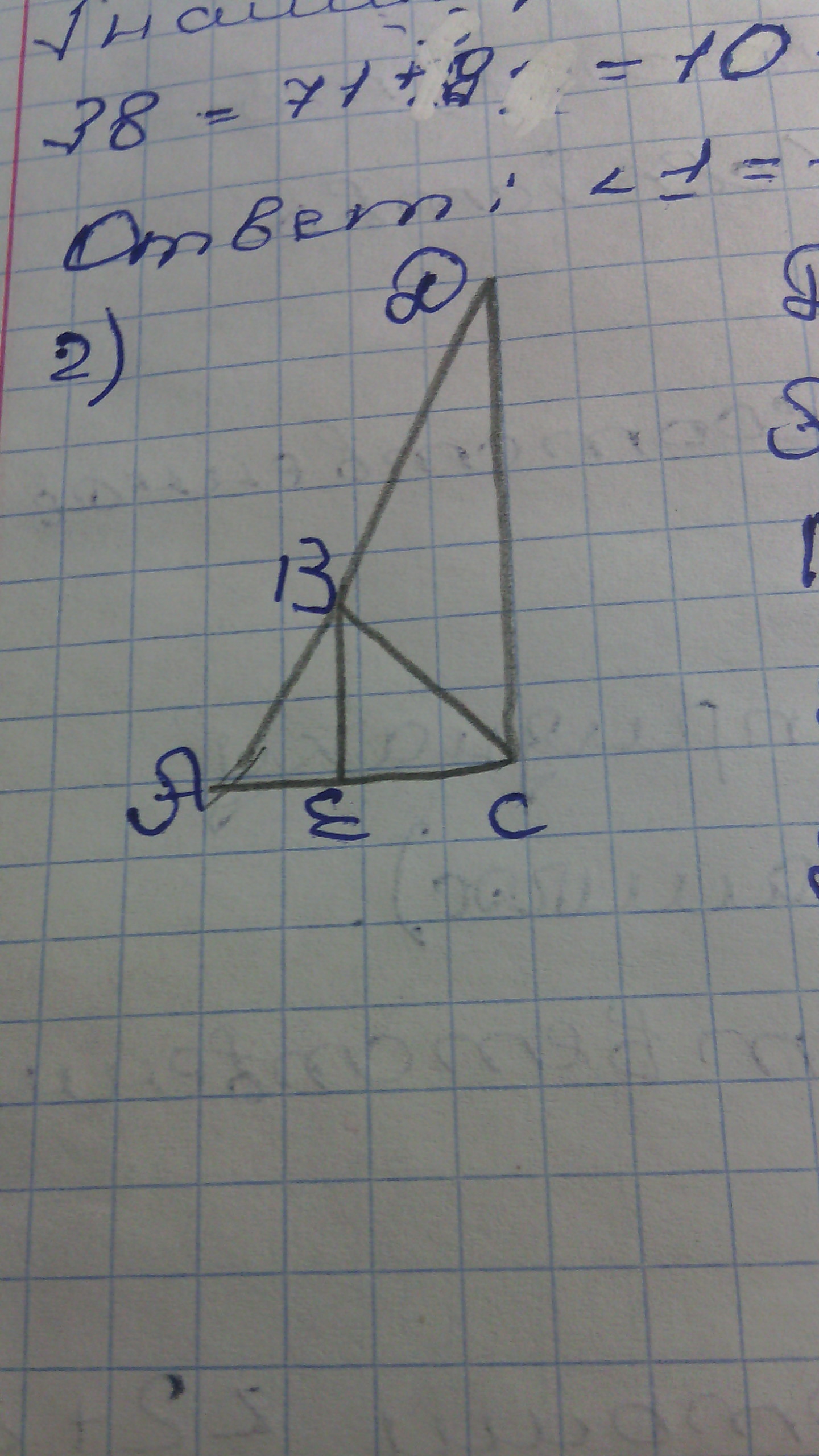
Ответы
Автор ответа:
0
Условие задачи неполное.
Дано: AB = BD = BC,
BE║DC.
Доказать: DC ⊥ AC .
Решение:
∠1 = ∠2 как соответственные при пересечении параллельных прямых ВЕ и DC секущей AD,
∠3 = ∠4 как накрест лежащие при пересечении параллельных прямых ВЕ и DC секущей ВС.
∠1 = ∠3 как углы при основании равнобедренного треугольника DBC, значит и
∠2 = ∠4.
Тогда ВЕ - биссектриса треугольника АВС, а, так как ΔАВС равнобедренный, то ВЕ и высота, т.е.
ВЕ⊥АС, а так как ВЕ║DC, то и DC⊥AC.
Приложения:
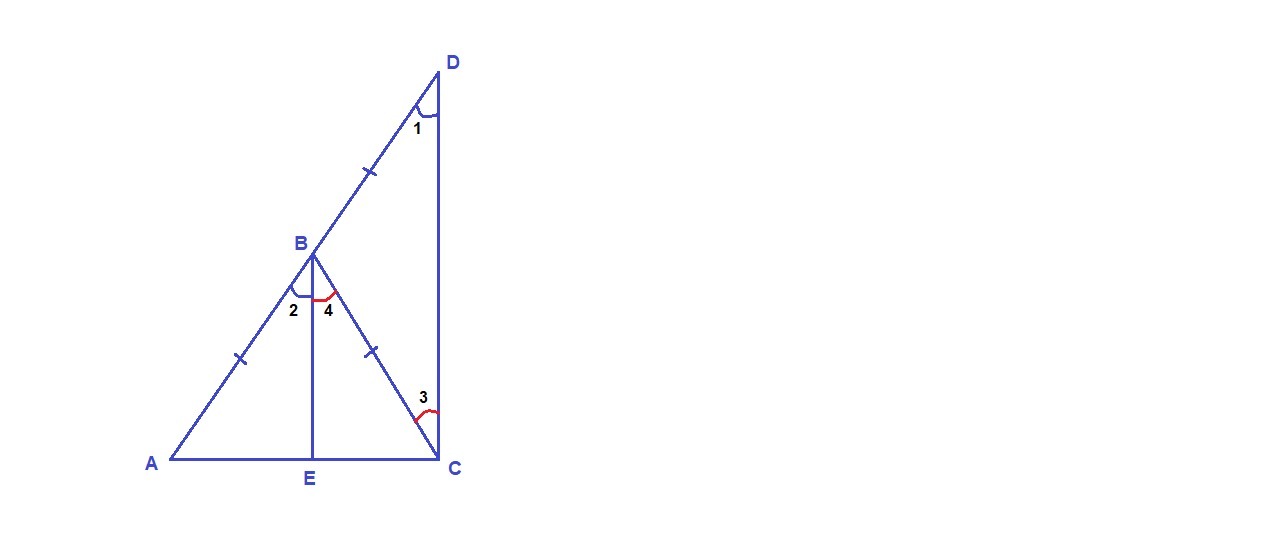
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: avek6464
Предмет: Математика,
автор: sapunmaks57
Предмет: Математика,
автор: манька703
Предмет: Математика,
автор: acermasha