Question

НУЖНО РЕШЕНИЕ ❤
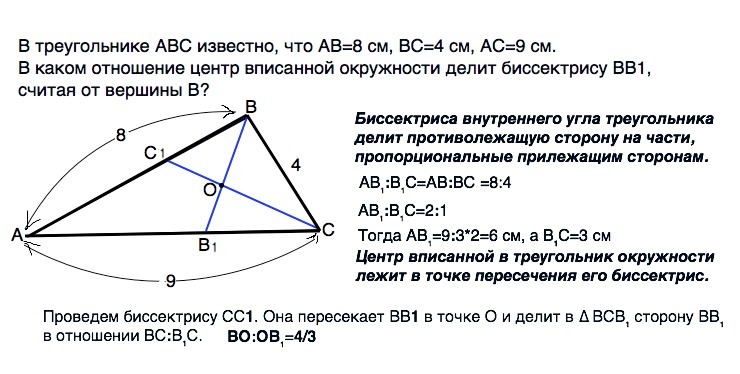
В треугольнике ABC известно, что AB=8 см, BC=4 см, AC=9 см. В каком отношение центр вписанной окружности делит биссектрису BB1, считая от вершины В?

Answer 1

Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.

АВ₁:В₁С=АВ:ВС=8:4

АВ₁:В₁С=2:1

Тогда АВ₁=9:3*2=6 см, а В₁С=3 см

Центр вписанной в треугольник окружности лежит в точке пересечения его биссектрис. 

Проведем биссектрису СС1. Она пересекает ВВ1 в точке О и делит в ∆ ВСВ₁ сторону ВВ₁ в отношении ВС:В₁С. 

ВО:ОВ₁=4/3