Question

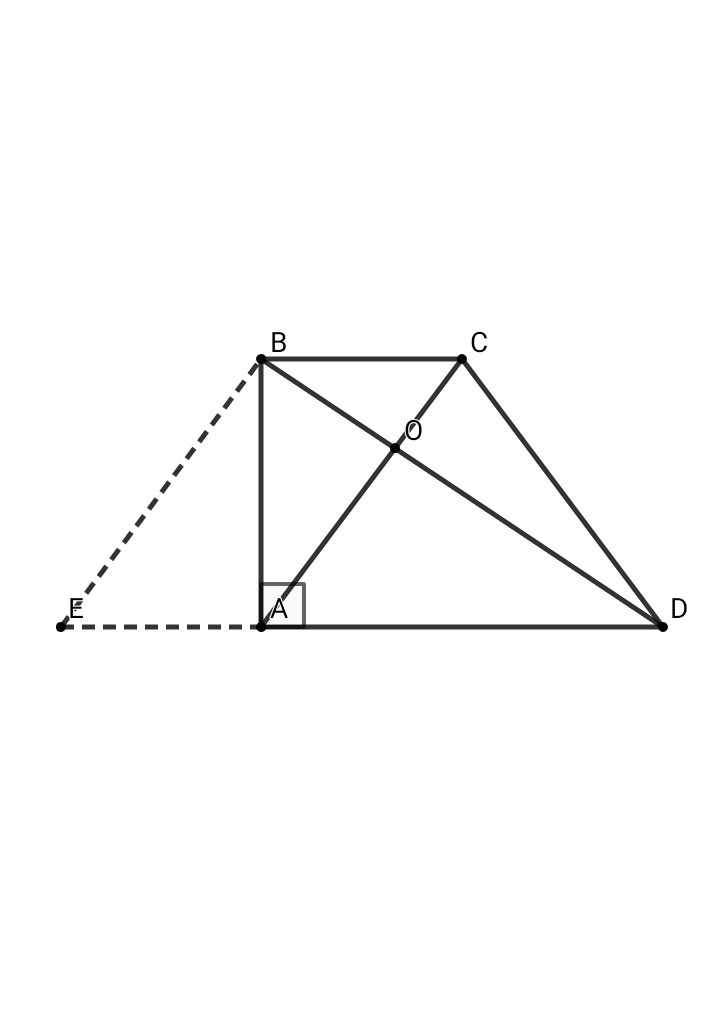
Диагонали прямоугольной трапеции ABCD взаимно перпендикулярны. Короткая боковая сторона AB равна 18 см, длинное основание AD равно 24 см.
1. Короткое основание BC:BC=   см. 2. Длины отрезков, на которые делятся диагонали в точке пересечения O: короткая диагональ делится на отрезки CO=   см и AO=    см. длинная диагональ делится на отрезки BO=   см и DO=   см.Ответить!

Answer 1

Из точки В проведём прямую ВЕ, параллельную диагонали АС, Е ∈ AD ⇒  BEAC - параллелограмм, ВС || ЕА, ВЕ || АС

Значит, ВС = ЕА , ВЕ = АС - по свойству параллелограмма

АС⊥BD - по условию, ВЕ || АС ⇒ ВЕ⊥BD, AB⊥ED

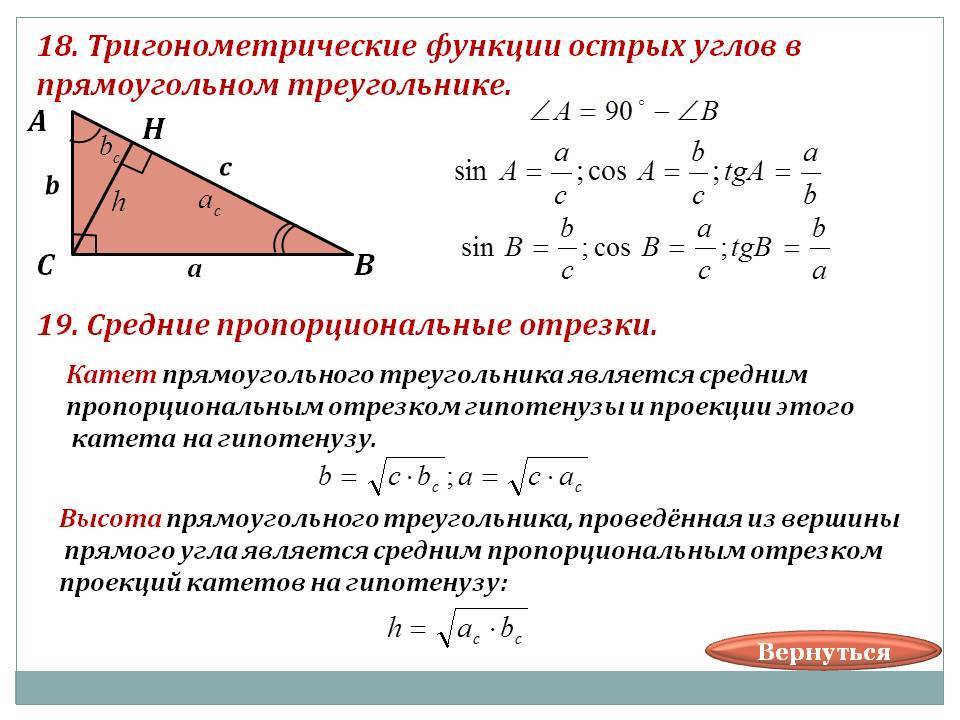
▪В ΔВЕD: пропорциональные отрезки в прямоугольном треугольнике ( см. приложение )

АВ² = ЕА • АD

EA = AB² / AD = 18² / 24 = 13,5 см

ВС = 13,5 см

▪В ΔBAD:  по теореме Пифагора

BD² = AB² + AD² = 18² + 24² = 6²•( 3² + 4² ) = 36•25 = 30²

BD = 30 см

AD² = OD • BD  ⇒  OD = AD² / BD = 24² / 30 = 576 / 30 = 19,2 см

BO = BD - OD = 30 - 19,2 = 10,8 см

▪В ΔBAD:  AO² = BO • OD = 10,8 • 19,2 = 207,36

AO = 14,4 см

▪В ΔАВС:  ВО² = АО • ОС  ⇒  ОС = ВО² / АО = 10,8² / 14,4 = 8,1

ОТВЕТ: ВС = 13,5 см ; СО = 8,1 см ; АО = 14,4 см ; ВО = 10,8 см ; DO = 19,2 см.