Предмет: Алгебра,
автор: denis35russ
Логарифмическое уравнение, решите плз
Приложения:
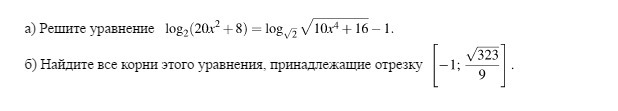
Ответы
Автор ответа:
0
ОДЗ:
Ответ:
Похожие вопросы
Предмет: История,
автор: valeriamoiseen3
Предмет: История,
автор: EnergyFR
Предмет: Математика,
автор: Leodemonzzz
Предмет: Математика,
автор: irvs