Предмет: Алгебра,
автор: ivanqwert2015
Решить предел функции (подробно пожалуйста!)
lim x->бесконечность (3x^2-2x+5)/(2x-1)^2
Приложения:
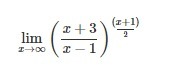
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: alinaprisaznuk85
Предмет: Геометрия,
автор: katti7774
Предмет: География,
автор: memworks2
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: Diar201415