Третья и последняя (на сегодня), выручайте!!!

Ответы
В конус вписан шар. Поверхность шара относится к площади основания как 4:3. Найти угол при вершине конуса.
Вариант решения.
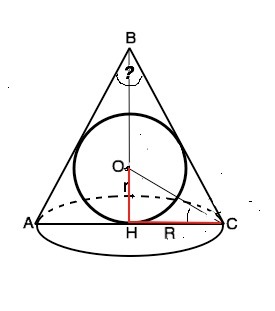
Сделаем рисунок-схему конуса с вписанным шаром с центром О и радиусом ОН=r .
∆ АВС - равнобедренный с боковыми сторонами - образующими конуса, и основанием - его диаметром.
ВН - высота конуса. СН=R- радиус его основания.
Площадь основания -πR²
Площадь сферы 4πr²
По условию 4πr²:πR² =4/3. После сокращения получаем r²/R² =1/3, откуда r/R=1/√3
В ∆ ОСН r/R=tg∠ВСН=1/√3, и это тангенс ∠=30°.
Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис. СО- биссектриса ∠ВСН. Следовательно ∠ВСН=2 ∠ОСН=60°
Тогда ∠ ВАС=∠BCA=60°, и искомый ∠АВС=60° или π/3.