Предмет: Алгебра,
автор: OlgaLaz08
Как это решать??????
Приложения:
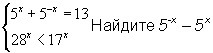
Ответы
Автор ответа:
0
Решим первое уравнение.
5^x=t>0;
t+(1/t)=13;
t^2-13t+1=0;
t_1=(13+√165)/2; t^2= (13-√165)/2;
x_1=log_5((13+√165)/2)>0
x_2=log_5((13-√165)/2)<0
Решим второе неравенство
28^x<17^x. Специалист, конечно сразу даст ответ, ну а мы немного помучаемся. (28/17)^x<(28/17)^0;
так как 28/17>1, это неравенство равносильно x<0⇒ из двух корней первого уравнения выберем второй.
Требуется найти 5^(-x_2)-5^(x_2)=1/t_2 - t_2=
2/(13-√165)-(13-√165)/2=(2(13+√165)/(169-165)-(13-√165)/2=√165
5^x=t>0;
t+(1/t)=13;
t^2-13t+1=0;
t_1=(13+√165)/2; t^2= (13-√165)/2;
x_1=log_5((13+√165)/2)>0
x_2=log_5((13-√165)/2)<0
Решим второе неравенство
28^x<17^x. Специалист, конечно сразу даст ответ, ну а мы немного помучаемся. (28/17)^x<(28/17)^0;
так как 28/17>1, это неравенство равносильно x<0⇒ из двух корней первого уравнения выберем второй.
Требуется найти 5^(-x_2)-5^(x_2)=1/t_2 - t_2=
2/(13-√165)-(13-√165)/2=(2(13+√165)/(169-165)-(13-√165)/2=√165
Автор ответа:
0
так как  , значит x<0.
, значит x<0.
Сделаем замену
Но, так как x<0, то новая переменная ограниченна нулем слева и единицей справа, т.е. .
.
Имеем:
Умножим на t обе части уравнения:




Так как , то имеем один корень уравнения, т.е.
, то имеем один корень уравнения, т.е.  .
.
Найдем значение выражения




Ответ:
Сделаем замену
Но, так как x<0, то новая переменная ограниченна нулем слева и единицей справа, т.е.
Имеем:
Умножим на t обе части уравнения:
Так как
Найдем значение выражения
Ответ:
Похожие вопросы
Предмет: Математика,
автор: fwolfard51
Предмет: Математика,
автор: lisachan2000
Предмет: Литература,
автор: sooprja
Предмет: Математика,
автор: Tan4ik2
Предмет: Биология,
автор: долгота