Предмет: Алгебра,
автор: sergei10052
А,б,в,г пожалуйста производная
Приложения:
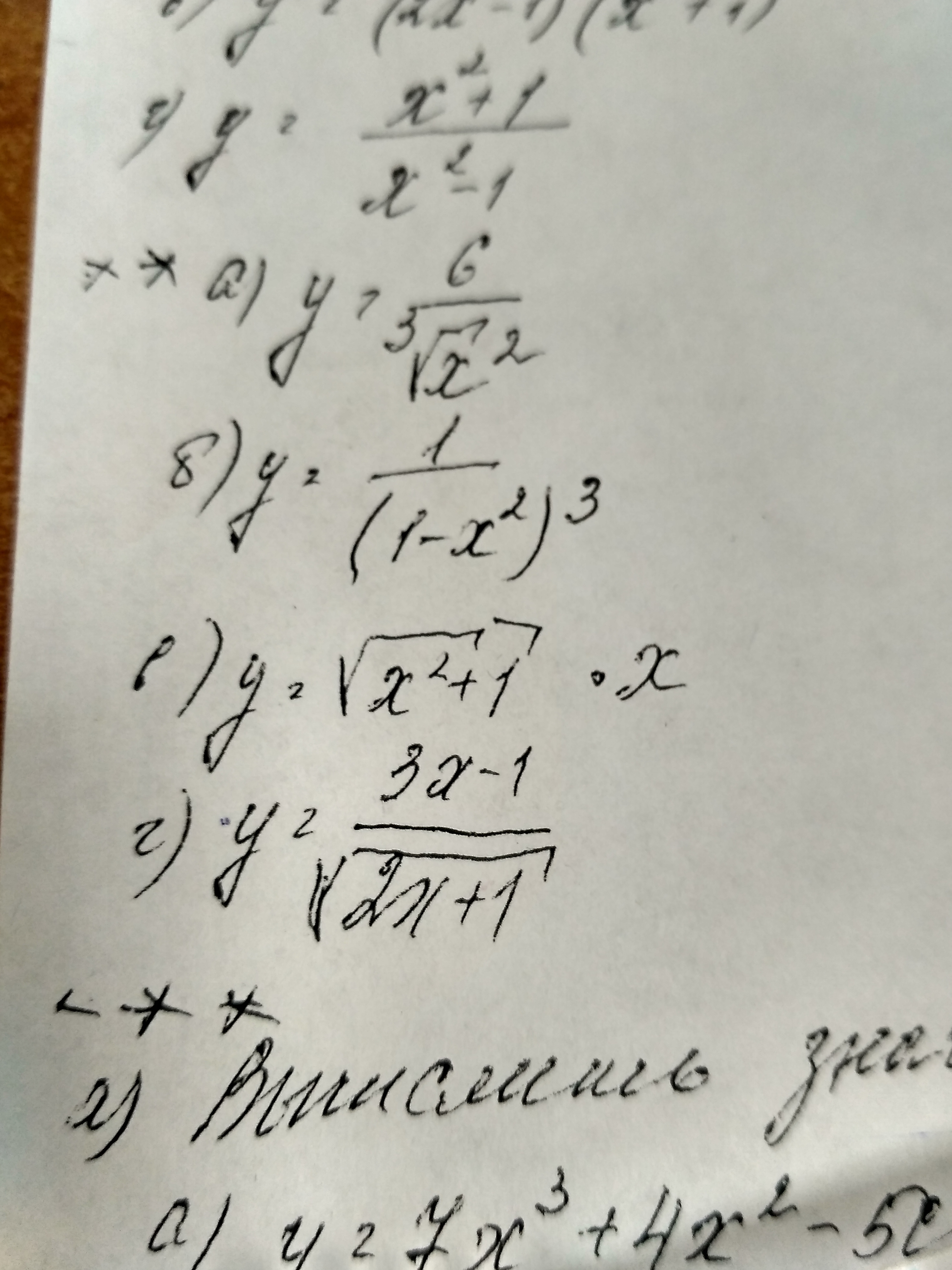
Ответы
Автор ответа:
0
а) y=6/x ^(2/3; y' =(6x^(-2/3))'=6*(-2/3)x^(-2/3-1)=-4x^(-5/3)=-4/∛x^5=-4/(x∛x^2; б) y=1/(1-x^2)^3
y =((1-x^2)^(-3) )'
y '=-3*(1-x^2)^(-4) *(1-x^2)' =(-3*(-2x)) /(1-x^2)^4=6x/(1-x^2)^4;
в) y=√(x^2+1) * x
y ' =(√(x^2+1)' *x+ √(x^2+1) *(x)'= 1/(2√(x^2+1)) *(x^2+1)' x+√(x^2+1)=
=2x/√(x^2+1) /(2√(x^2+1) +√(x^2+1)=(x+x^2+1) /√(x^2+1)
г)y '=((3x-1)'(√(2x+1) - (3x-1)(√(2x+1)') /(√(2x+1)^2=
=(3√(2x+1) -(3x-1)*1/(2√(2x+1)) *(2x+1)' ) / (2x+1)=
=(3√(2x+1 ) - 1/√(2x+1) ) /(2x+1)=((3*(2x+1)-1) /√(2x+1) ) / (2x+1)=
=(6x+2)/(√(2x+1) *(2x+1))
y =((1-x^2)^(-3) )'
y '=-3*(1-x^2)^(-4) *(1-x^2)' =(-3*(-2x)) /(1-x^2)^4=6x/(1-x^2)^4;
в) y=√(x^2+1) * x
y ' =(√(x^2+1)' *x+ √(x^2+1) *(x)'= 1/(2√(x^2+1)) *(x^2+1)' x+√(x^2+1)=
=2x/√(x^2+1) /(2√(x^2+1) +√(x^2+1)=(x+x^2+1) /√(x^2+1)
г)y '=((3x-1)'(√(2x+1) - (3x-1)(√(2x+1)') /(√(2x+1)^2=
=(3√(2x+1) -(3x-1)*1/(2√(2x+1)) *(2x+1)' ) / (2x+1)=
=(3√(2x+1 ) - 1/√(2x+1) ) /(2x+1)=((3*(2x+1)-1) /√(2x+1) ) / (2x+1)=
=(6x+2)/(√(2x+1) *(2x+1))
Похожие вопросы
Предмет: Физика,
автор: nigarism08
Предмет: Математика,
автор: polinazua
Предмет: Биология,
автор: maxim06855
Предмет: Математика,
автор: ангел378
Предмет: Математика,
автор: 737Ира