Question

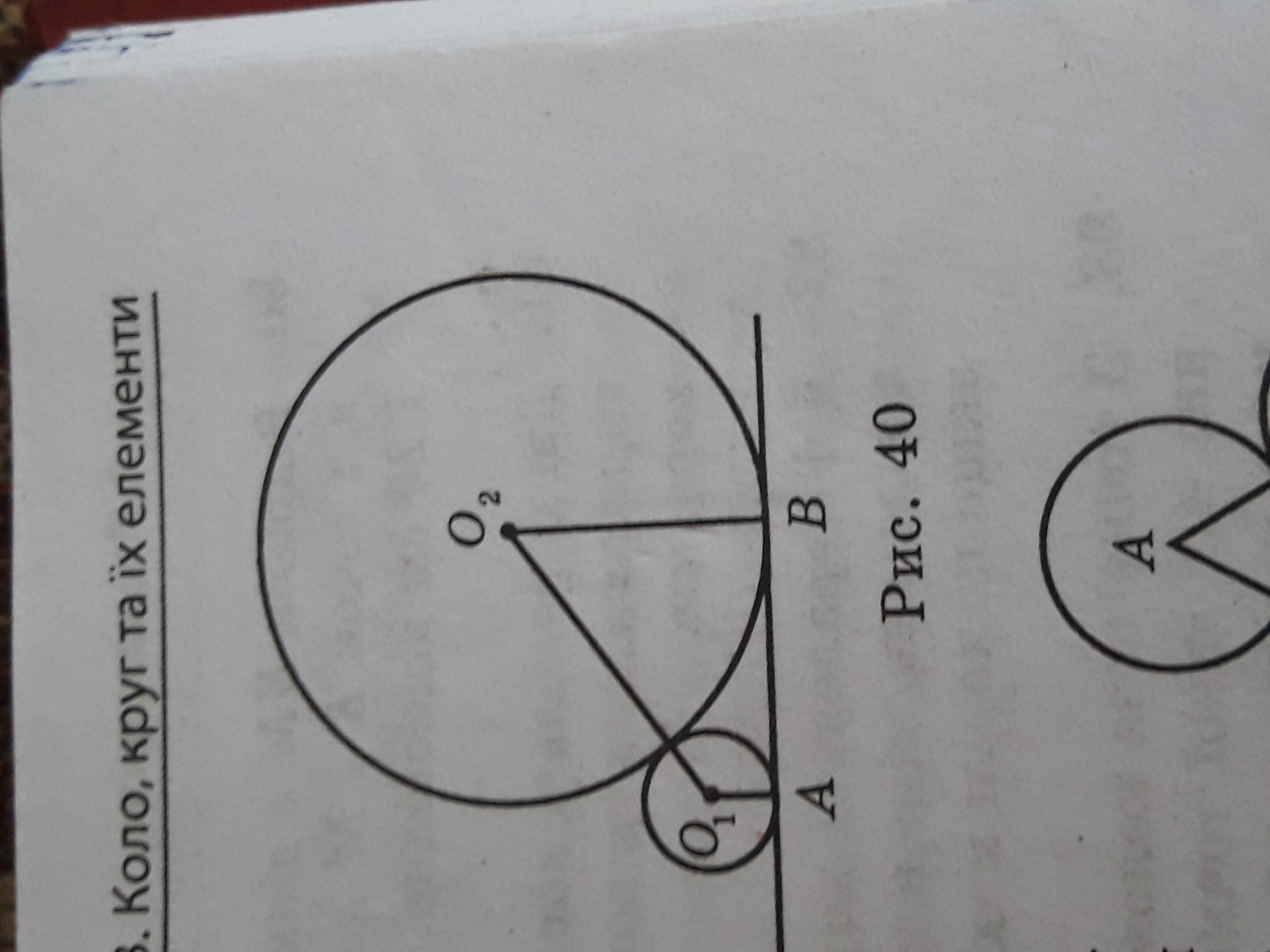
Две окружности, которие касаются между собой, касаются прямой. Известно, что O2B = AB = 8 см. Найти длину отрезка O1A.
Рисунок во вложении

Answer 1

Пусть радиус первой окружности равен r, тогда O_1O_2=r+8.
Опустим перпендикуляр O_1C на O_2B, тогда AO_1CB - прямоугольник; O_1A=CB=r; O_1C=AB=8; O_2C=8-r. Из прямоугольного треугольника O_1O_2C по теореме Пифагора получаем 
(r+8)^2=(8-r)^2+8^2; r^2+16r+64=64-16r+r^2+64;
32r=64; r=2; O_1A=2 

Ответ: 2