Предмет: Алгебра,
автор: alexcool0207148
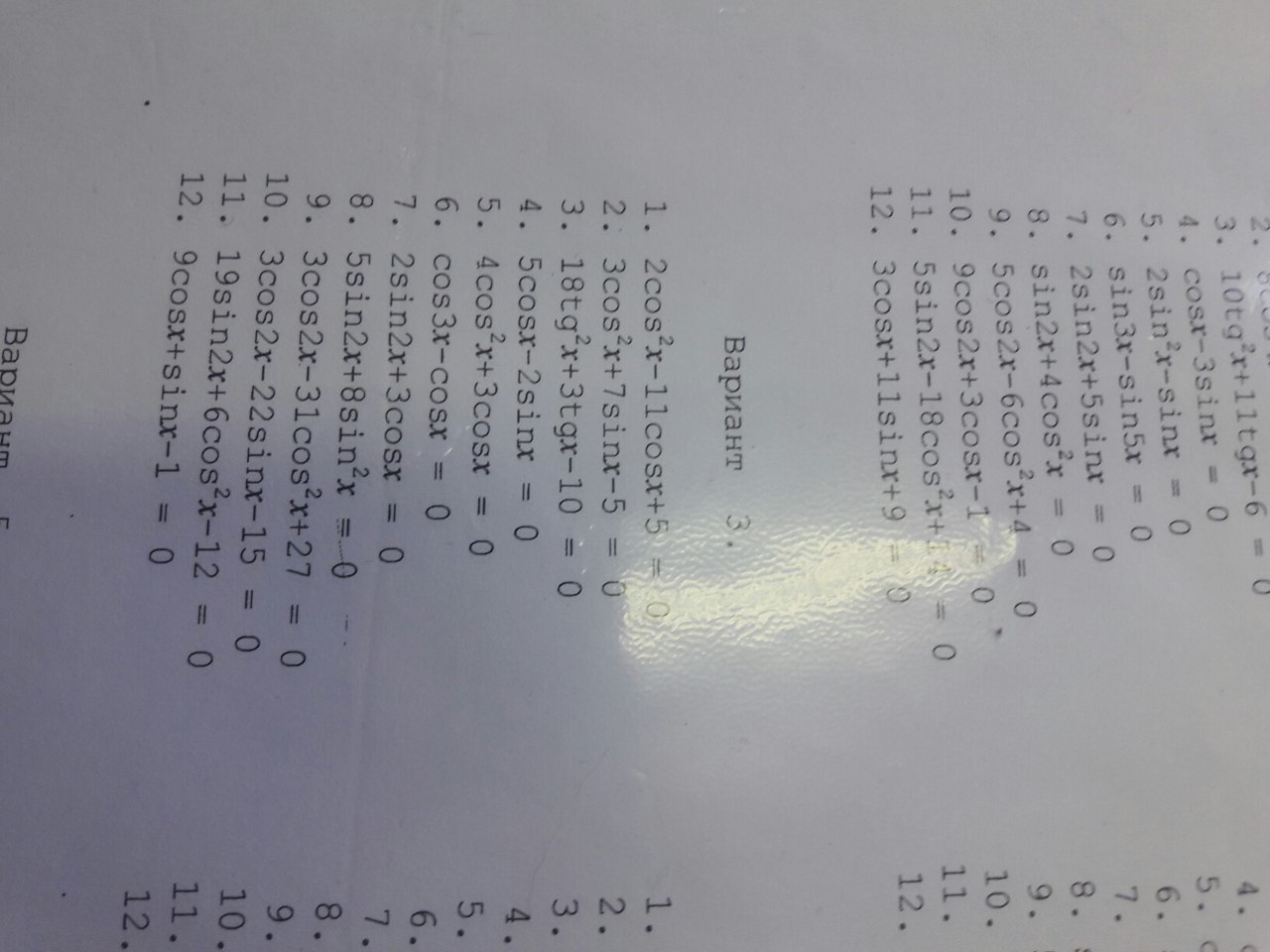
Помогите решить пожалуйста тригонометрические уравнения.Вариант 3
Приложения:
Ответы
Автор ответа:
0
1. Пусть cosх=у. Тогда : 2у^2 - 11у + 5=0 .
д=121-4*5*2= 121-40=81.
у1=(11+9)/2*2=5. у2=(11-9)/2*2= 1/2.
При у=5. соsх=5.Нет корней.
При у=1/2 соsх=1/2. х= arccos1/2+2пиn,n принадлежит z. x=пи/3+2пиn,n принадлежит z.
2. Используем основное тригонометрическое тождество . получаем: 3(1-sin^2x)+7sinx - 5 =0.
3-3sin^2x+7sinx - 5=0.
-3sin^2x+7sinx -2=0.
3sin^2x-7sinx +2=0.
Пусть sinх=у. Тогда :3y^2-7y+2=0.
d=49-4*3*2=25.
y1=(7+5)/2*3=2.y2=(7-5)/2*3=1/3.
При у=1/3 sinх=1/3. х= (-1)^n arcsin1/3+пиn,n принадлежит z..При у=2.sinх=2.Нет корней.
д=121-4*5*2= 121-40=81.
у1=(11+9)/2*2=5. у2=(11-9)/2*2= 1/2.
При у=5. соsх=5.Нет корней.
При у=1/2 соsх=1/2. х= arccos1/2+2пиn,n принадлежит z. x=пи/3+2пиn,n принадлежит z.
2. Используем основное тригонометрическое тождество . получаем: 3(1-sin^2x)+7sinx - 5 =0.
3-3sin^2x+7sinx - 5=0.
-3sin^2x+7sinx -2=0.
3sin^2x-7sinx +2=0.
Пусть sinх=у. Тогда :3y^2-7y+2=0.
d=49-4*3*2=25.
y1=(7+5)/2*3=2.y2=(7-5)/2*3=1/3.
При у=1/3 sinх=1/3. х= (-1)^n arcsin1/3+пиn,n принадлежит z..При у=2.sinх=2.Нет корней.
Похожие вопросы
Предмет: Русский язык,
автор: khomutovivan2409
Предмет: Алгебра,
автор: Loregme
Предмет: История,
автор: ksyniatko
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: YuliaLay