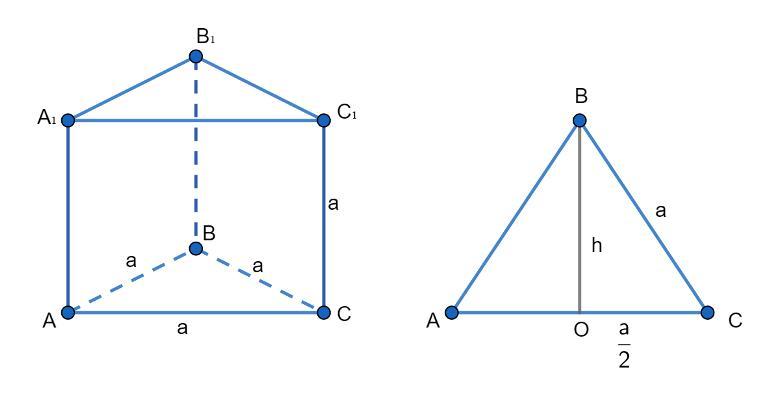
Длины всех ребер прямой треугольной призмы равны. Вычислите обьем призмы, если периметр ее боковой грани равен 48см
Ответы
Ответ:
Объем призмы равен 432√3 см³.
Пошаговое объяснение:
Так как по условию длины всех ребер треугольной призмы равны, то в основании лежит правильный треугольник, а каждая боковая грань является квадратом.
1) По условию периметр боковой грани равен 48 см.
P = 4a = 48 см, a = 48 см /4 = 12 см. Каждое ребро равно 12 см. (a - длина ребра призмы).
2) Объем призмы равен произведению площади основания на высоту призмы. V = Sосн * H.
Призма прямая, поэтому ее высота равна длине бокового ребра. H = a = 12 см.
Найдем площадь основания, т.е. площадь равностороннего ΔABC. Sосн = 1/2 * a * h.
Высота в равностороннем треугольнике (h) является биссектрисой и медианой.
По теореме Пифагора из прямоугольного ΔBOC найдем высоту основания: h = √(a²-a²/4) = √(3a²/4) = (a/2) *√3 = (12/2)*√3 см = 6√3 см.
Площадь основания Sосн = 1/2 * a * h = 1/2 * 12 * 6√3 см² = 36√3 см².
Объем призмы: V = Sосн * H = 36√3 см² * 12 см = 432√3 см³.