Question

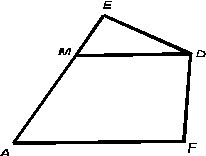
На рисунке AM=MD,DE=DF,AE=AF. Доказать : MD||AF. 

Answer 1

Треугольники AEF и DEF равнобедренные, поэтому высоты-медианы-биссектрисы, проведённые из вершин A и D соответственно, проходят через середину EF, то есть обе принадлежат прямой AD. Значит, AD — биссектриса угла EAF, ∠MAD = ∠FAD. Треугольник AMD равнобедренный, ∠MDA = ∠MAD. Получаем:  

 

∠MDA = ∠MAD = ∠FAD.  

 

Внутренние накрест лежащие углы при прямых MD и AF и секущей AD равны. Следовательно, MD ∥ AF