Предмет: Алгебра,
автор: alina70ss
Найдите область определения функций
Распишите пожалуйста
Приложения:
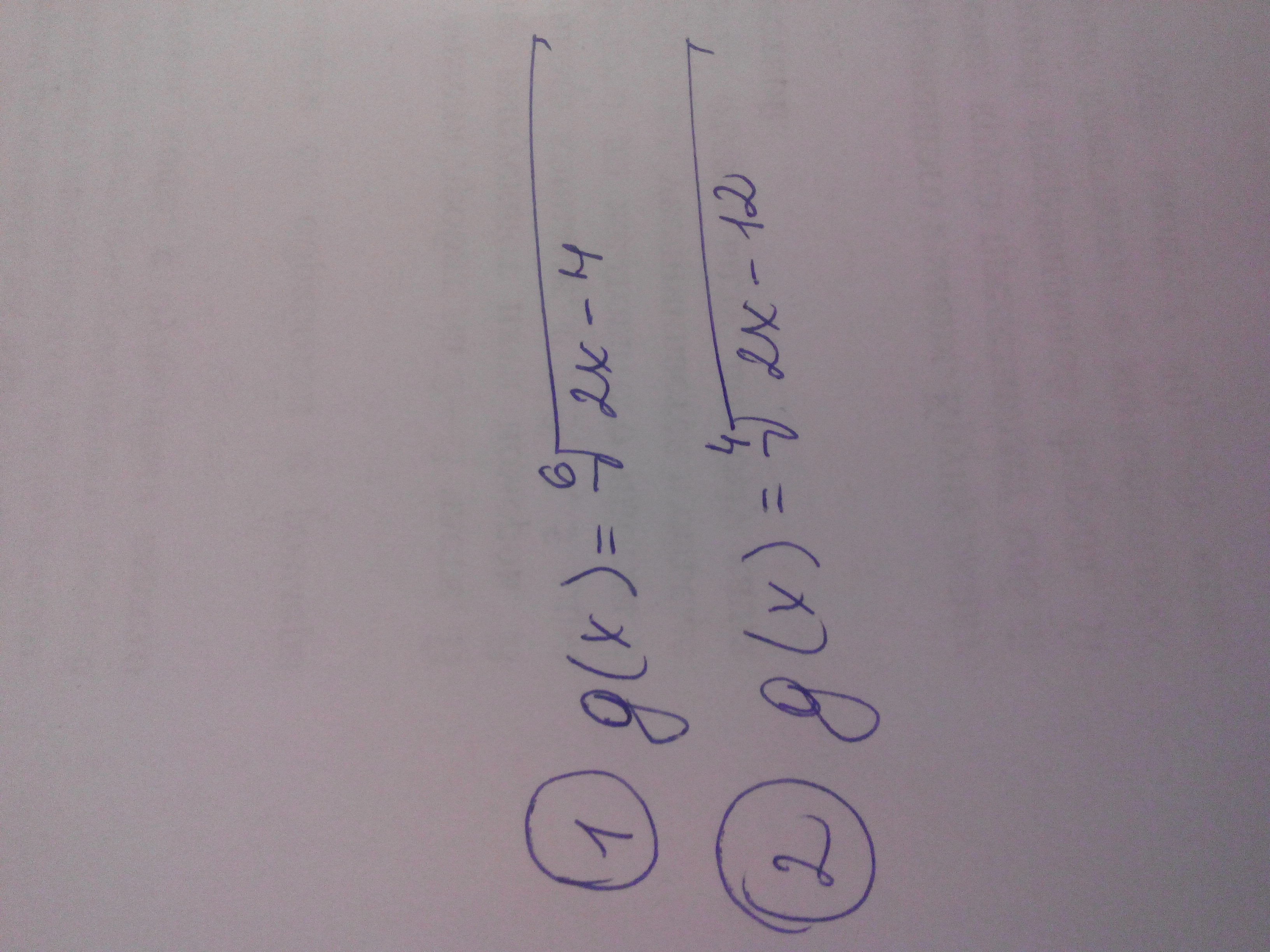
Ответы
Автор ответа:
0
в обеих функциях корни четной степени значит подкоренное выражение должно быть положительным
g(x)=⁶√(2x-4) 2x-4≥0 2x≥4 x≥2 x∈[2;+∞)
g(x)=⁴√(2x-12) 2х-12≥0 2х≥12 х≥6 х∈[6;+∞)
g(x)=⁶√(2x-4) 2x-4≥0 2x≥4 x≥2 x∈[2;+∞)
g(x)=⁴√(2x-12) 2х-12≥0 2х≥12 х≥6 х∈[6;+∞)
Похожие вопросы
Предмет: Английский язык,
автор: 281782
Предмет: Математика,
автор: valerakrivenko79
Предмет: Литература,
автор: catliza259
Предмет: Математика,
автор: Барсикбарсик
Предмет: Математика,
автор: рыбка05