Предмет: Математика,
автор: DuOlya
Логарифмічні нерівності.
Приложения:
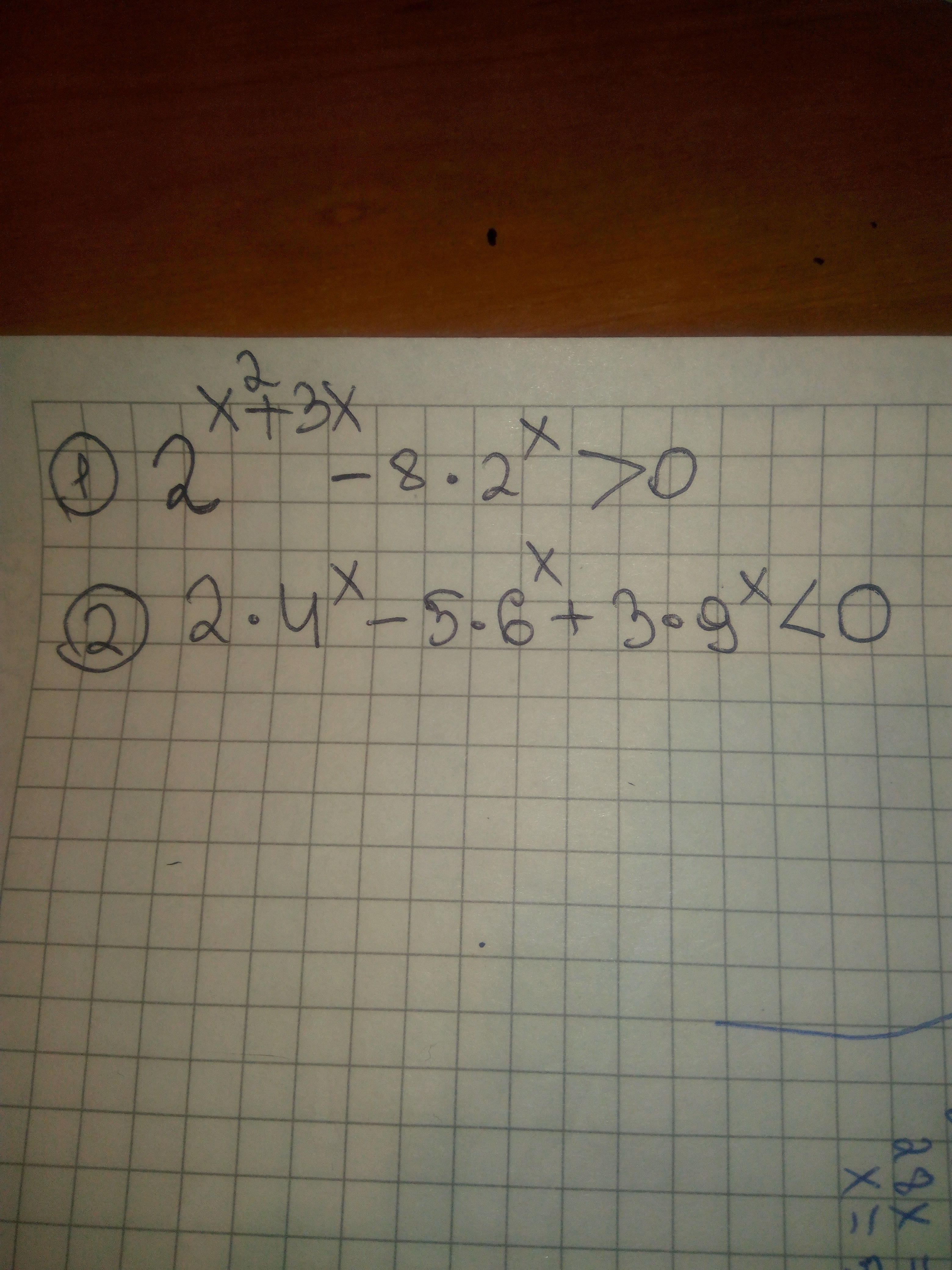
Ответы
Автор ответа:
0
1
2^(x²+3x)-2^(x+3)>0
2^(x²+3x)>2^(x+3)
x²+3x>x+3
x²+2x-3>0
x1+x2=-2 U x1*x2=-3
x1=-3 U x2=1
x∈(-∞;-3) U (1;∞)
2
2*2^2x-5*2^x*3^x+3*3^2x<0/3^2x
2*(2/3)^2x-5*(2/3)^x+3<0
(2/3)^x=a
2a²-5a+3<0
D=25-24=1
a1=(5-1)/4=1
a2=(5+1)/2=3/2
1<(2/3)^x<3/2
-1<x<0
x∈(-1;0)
2^(x²+3x)-2^(x+3)>0
2^(x²+3x)>2^(x+3)
x²+3x>x+3
x²+2x-3>0
x1+x2=-2 U x1*x2=-3
x1=-3 U x2=1
x∈(-∞;-3) U (1;∞)
2
2*2^2x-5*2^x*3^x+3*3^2x<0/3^2x
2*(2/3)^2x-5*(2/3)^x+3<0
(2/3)^x=a
2a²-5a+3<0
D=25-24=1
a1=(5-1)/4=1
a2=(5+1)/2=3/2
1<(2/3)^x<3/2
-1<x<0
x∈(-1;0)
Похожие вопросы
Предмет: Русский язык,
автор: derpstudios098
Предмет: Математика,
автор: zibekasylbekova019
Предмет: Алгебра,
автор: lifiifog
Предмет: Математика,
автор: bordonosova1976
Предмет: Геометрия,
автор: food73838