Предмет: Алгебра,
автор: LitaKolt
а)решить уравнение -корень sin(-5pi/2 +x)*sinx=cos x
б)найдите все корни(3) уравнения в промежутке (9pi/2;6pi)включая обе точки
решение:
-корень sin(-5pi/2 +x)*sinx=cos x
-корень sin(-5pi/2 +x)*sinx=0 ; cos x=0
sin(-5pi/2 +x)*sinx=корень2 x=pi/2 +pin,n принадлежит Z
как дальше?
Ответы
Автор ответа:
0
верное уравнение:



отбор корней
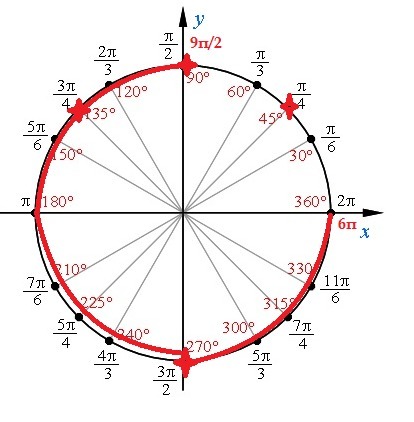
(см. рисунок)
х= п/2 +пn попадает на интервал дважды
это будут точки х= 9п/2 и х= 11п/2
х=п/4+2пn не попадает на интервал
х=3п/4 +2 пn попадает на интервал и это будет точка

отбор корней
(см. рисунок)
х= п/2 +пn попадает на интервал дважды
это будут точки х= 9п/2 и х= 11п/2
х=п/4+2пn не попадает на интервал
х=3п/4 +2 пn попадает на интервал и это будет точка
Приложения:
Похожие вопросы
Предмет: Оʻzbek tili,
автор: nargiz19872305
Предмет: Русский язык,
автор: aruzandzangirbaeva
Предмет: Геометрия,
автор: ivansklyar2008
Предмет: Биология,
автор: Алиман
Предмет: Биология,
автор: dashylkaa