Предмет: Алгебра,
автор: Maryashc
помогите пожалуйста с алгеброй
Приложения:
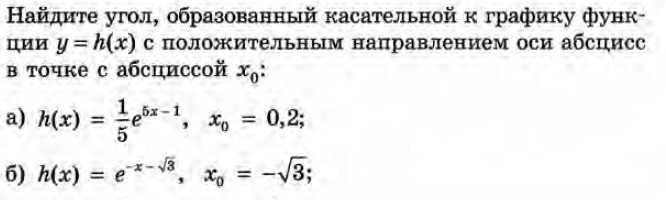
Ответы
Автор ответа:
0
Уравнение касательной в точке x0: y=h(x0)+h '(x0)(x -x0), где коэффициент при x, h'(x0) =tga - это тангенс угла между касательной и осью абсцисс.
a) h'(x)=((1/5)e^(5x-1))'=((5x-1)'/5)e^(5x-1)=(5/5)e^(5x-1)=e^(5x-1)
h'(x0)=e^(5*0,2-1)=e^0=1, tga=1, a=π/4=45°
б) h'(x)= (-x-√3)'e^(-x-√3)= -e^(-x-√3)
h'(x0)= -e^(√3-√3)= -e^0= -1, tga= -1, a=3π/4=135°
a) h'(x)=((1/5)e^(5x-1))'=((5x-1)'/5)e^(5x-1)=(5/5)e^(5x-1)=e^(5x-1)
h'(x0)=e^(5*0,2-1)=e^0=1, tga=1, a=π/4=45°
б) h'(x)= (-x-√3)'e^(-x-√3)= -e^(-x-√3)
h'(x0)= -e^(√3-√3)= -e^0= -1, tga= -1, a=3π/4=135°
Похожие вопросы