Предмет: Алгебра,
автор: AnChi16
Помогите с системой!
Приложения:
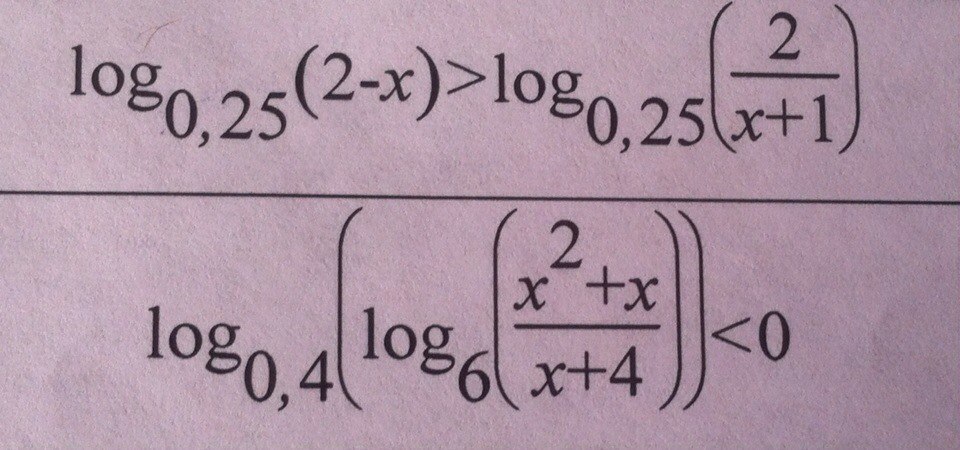
Ответы
Автор ответа:
0
Решение 2 неравенства x∈(-4;-3)U(8;+∞)
Решение 1 неравенства x∈(-1;0)U(1;2)
Области не пересекаются ⇒
Ответ ∅
Смотри на фото решение
Решение 1 неравенства x∈(-1;0)U(1;2)
Области не пересекаются ⇒
Ответ ∅
Смотри на фото решение
Приложения:


Автор ответа:
0
1
ОДЗ
{2-x>0⇒x<2
{x+1>0⇒x>-1
x∈(-1;2)
основание меньше 1,знак меняется
(2-x)<2/(x+1)
(2-x)-2/(x+1)<0
*2x-x²+2-x-2)/(x+1)<0
(x²-x)/(x+1)>0
x(x-1)/(x+1)>0
x=0 x=1 x=-1
_ + _ +
------------------(-1)-------------(0)-----------------------------(1)----------------------
-1<x<0 U x>1 +ОДЗ
x∈(-1;0) U (1;2)
2
ОДЗ
{x(x+1)/(x+4)>0
{log(6)[(x²+x)/(x+4)]>0⇒(x²+x)/(x+4)>1
1)x=0 x=-1 x=-4
_ + _ +
------------------(-4)-------------(-1)-------------------(0)----------------------
-4<x<-1 U x>0
2)(x²+x)/(x+4)-1>0
(x²+x-x-4)/(x+4)>0
(x-2)(x+2)/(x+4)>0
x=2 x=-2 x=-4
_ + _ +
------------------(-4)-------------(-2)----------------------(2)----------------------
-4<x<-2 U x>2
x∈(-4;-2) U (2;∞)
log(0,4)log(6)[(x²+x)/(x+4)]<0
Основание меньше 1,знак меняется
log(6)[(x²+x)/(x+4)]>1
[(x²+x)/(x+4)]>6
[(x²+x)/(x+4)]-6>0
(x²+x-6x-24)/(x+4)>0
(x²-5x-24)/(x+4)>0
x²-5x-24=0
x1+x2=5 U x1*x2=-24⇒x=-3 U x=8
x+4=0⇒x=-4
_ + _ +
-------------------(-4)-------------------(-3)----------------(8)----------------------
-4<x<-3 U x>8 + ОДЗ
x∈(-4;-3) U (8;∞)
ОДЗ
{2-x>0⇒x<2
{x+1>0⇒x>-1
x∈(-1;2)
основание меньше 1,знак меняется
(2-x)<2/(x+1)
(2-x)-2/(x+1)<0
*2x-x²+2-x-2)/(x+1)<0
(x²-x)/(x+1)>0
x(x-1)/(x+1)>0
x=0 x=1 x=-1
_ + _ +
------------------(-1)-------------(0)-----------------------------(1)----------------------
-1<x<0 U x>1 +ОДЗ
x∈(-1;0) U (1;2)
2
ОДЗ
{x(x+1)/(x+4)>0
{log(6)[(x²+x)/(x+4)]>0⇒(x²+x)/(x+4)>1
1)x=0 x=-1 x=-4
_ + _ +
------------------(-4)-------------(-1)-------------------(0)----------------------
-4<x<-1 U x>0
2)(x²+x)/(x+4)-1>0
(x²+x-x-4)/(x+4)>0
(x-2)(x+2)/(x+4)>0
x=2 x=-2 x=-4
_ + _ +
------------------(-4)-------------(-2)----------------------(2)----------------------
-4<x<-2 U x>2
x∈(-4;-2) U (2;∞)
log(0,4)log(6)[(x²+x)/(x+4)]<0
Основание меньше 1,знак меняется
log(6)[(x²+x)/(x+4)]>1
[(x²+x)/(x+4)]>6
[(x²+x)/(x+4)]-6>0
(x²+x-6x-24)/(x+4)>0
(x²-5x-24)/(x+4)>0
x²-5x-24=0
x1+x2=5 U x1*x2=-24⇒x=-3 U x=8
x+4=0⇒x=-4
_ + _ +
-------------------(-4)-------------------(-3)----------------(8)----------------------
-4<x<-3 U x>8 + ОДЗ
x∈(-4;-3) U (8;∞)
Приложения:


Похожие вопросы
Предмет: Английский язык,
автор: Sygex
Предмет: Физика,
автор: leha83452
Предмет: Информатика,
автор: adiya2673
Предмет: Литература,
автор: anechka10s