Question

Че­ло­век стоит на рас­сто­я­нии 12 м от стол­ба, на ко­то­ром висит фо­нарь, рас­по­ло­жен­ный на вы­со­те 9,5 м. Тень че­ло­ве­ка равна 3 м. Ка­ко­го роста че­ло­век (в мет­рах)?

Answer 1

Ответ:

1,9 м

Пошаговое объяснение:

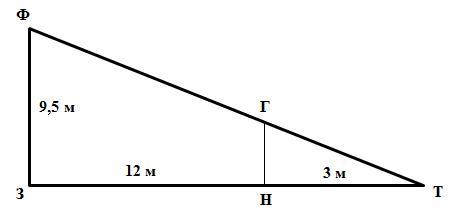
Введём обозначения (см. рисунок):

Ф - где фонарь висит, З - земля, Г - конец головы человека, Н - конец ноги человека, Т - тень человека. Тогда задачу можем оформить следующим образом:

Дано:

В ΔФЗТ:

∠З = 90°

ФЗ = 9,5 м

ЗН = 12 м

НТ = 3 м

Найти ГН.

Решение. Так как ∠ГНТ = 90° и ∠Ф = ∠НГТ , то треугольники ΔФЗТ и ΔГНТ подобны. Тогда по свойству подобных треугольников

ГН : ФЗ = НТ : ЗТ.  

Отсюда ГН = (НТ · ФЗ) : ЗТ = (3 м · 9,5 м) : (ЗН + НТ)=

=(3 м · 9,5 м) : (12 м + 3 м)=28,5 м : 15 = 1,9 м