Question

Один из внешних углов треугольника равен 90 градусам. Углы не смежные с данным углом, относятся как 1:4. Найдите наибольший из них. Ответ дайте в градусах.

Answer 1

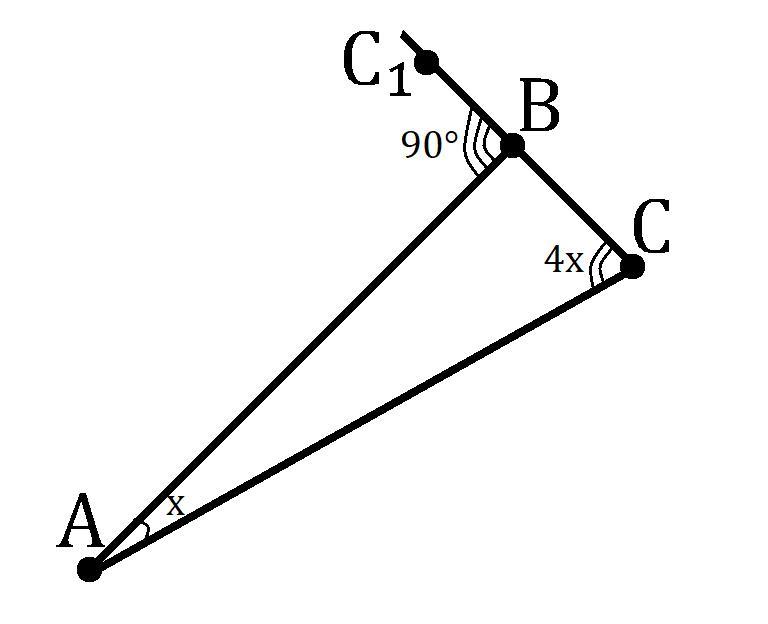
Дано: ∠ABC₁ = 90°; ∠BAC : ∠ACB = 1 : 4.

Найти: ∠ACB.

Решение:

Пусть ∠BAC=x, тогда из отношения следует, что ∠ACB=4x.

∠ABC₁+∠ABC=180° как сумма смежных углов;

∠ABC = 180°-∠ABC₁ = 180°-90° = 90°.

∠ABC+∠ACB+∠BAC=180° как сумма углов в треугольнике.

∠ABC = 180°-∠ACB-∠BAC = 180°-5x.

Составим уравнение и решим его:

180°-5x = 90°;  5x = 90°;  x = 18°.

∠ACB = 4x = 4·18° = 72°.

Ответ: 72°.