Question

найдите высоты равнобедренного треугольника,если его боковая сторона равна 17 см,а основание 30 см

Answer 1

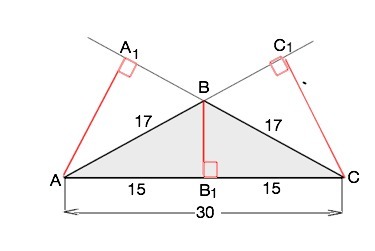
   Назовём данный треугольник АВС.

ВВ1- высота к АС.

АА1=СС1 - высоты к равным боковым сторонам.

   Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒

АВ1=СВ1=30:2=15 см

∆ АВВ1=∆ СВВ1 ( по трем сторонам).

Из ∆ АВВ1 по т.Пифагора

   ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см

Высоты к боковым сторонам найдем из площади ∆ АВС

   Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его. 

S(ABC)=BB1•AC:2=8•15=120 см²

AA1=2S(ABC):BC

   AA1=CC1=$frac{240}{17} =14 frac{2}{17}$ см