Предмет: Алгебра,
автор: spokets99
Помогите решить неравенства
Приложения:
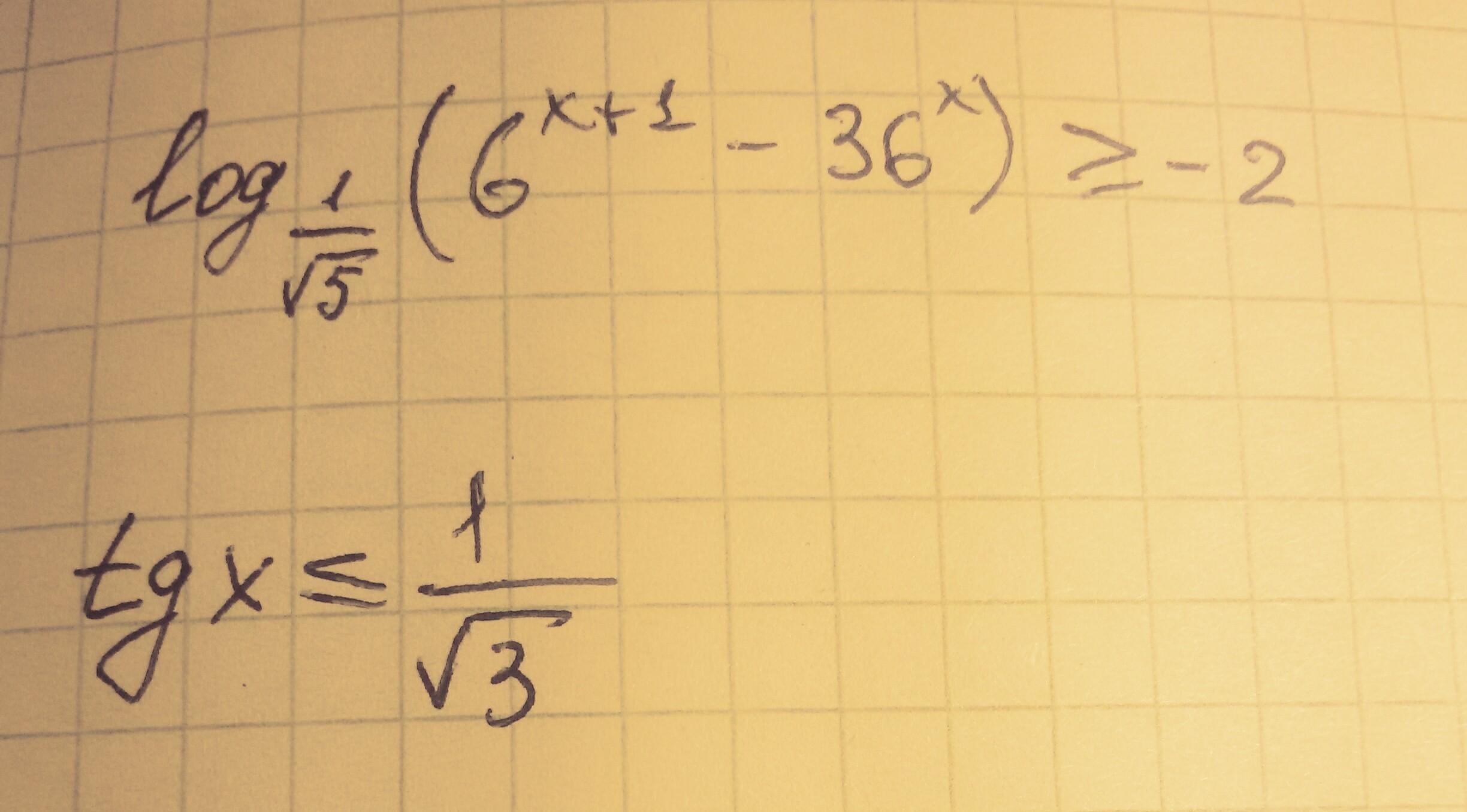
Ответы
Автор ответа:
0
log₁/√₅(6ˣ⁺¹-36ˣ)≤-2
ОДЗ: 6ˣ⁺¹-36ˣ>0 6*6ˣ-6²ˣ>0 6ˣ*(6-6ˣ)>0 6-6ˣ>0 6ˣ<6¹ x<1
1/√5≈0,45<0 ⇒
6ˣ⁺¹-36ˣ≥(1/√5)⁻²
6*6ˣ-6²ˣ≥5
6x²-6*6ˣ+5≤0
6ˣ=t
t²-6t+5≤0
t²-6t+5=0 D=16
t₁=1 6ˣ=1
t₂=5 6ˣ=5 ⇒
(6ˣ-1)(6ˣ-5)≤0
x<1
6ˣ-1≥0 6ˣ≥1 x≥0
6ˣ-5≤0 6ˣ≤5 x≤log₆5≈0,9
x∈[log₆5;1).
x<1
6ˣ-1≤0 6ˣ≤1 x≤0
6ˣ-5≥0 6ˣ≥0 x≥log₆5≈0,9
x∈(-∞;0]. ⇒
Ответ: x∈(-∞;0]U[log₆5;1).
tgx≤1/√3
tgx≤√3/3
x∈[π/2+πn;7π/6+πn]
ОДЗ: 6ˣ⁺¹-36ˣ>0 6*6ˣ-6²ˣ>0 6ˣ*(6-6ˣ)>0 6-6ˣ>0 6ˣ<6¹ x<1
1/√5≈0,45<0 ⇒
6ˣ⁺¹-36ˣ≥(1/√5)⁻²
6*6ˣ-6²ˣ≥5
6x²-6*6ˣ+5≤0
6ˣ=t
t²-6t+5≤0
t²-6t+5=0 D=16
t₁=1 6ˣ=1
t₂=5 6ˣ=5 ⇒
(6ˣ-1)(6ˣ-5)≤0
x<1
6ˣ-1≥0 6ˣ≥1 x≥0
6ˣ-5≤0 6ˣ≤5 x≤log₆5≈0,9
x∈[log₆5;1).
x<1
6ˣ-1≤0 6ˣ≤1 x≤0
6ˣ-5≥0 6ˣ≥0 x≥log₆5≈0,9
x∈(-∞;0]. ⇒
Ответ: x∈(-∞;0]U[log₆5;1).
tgx≤1/√3
tgx≤√3/3
x∈[π/2+πn;7π/6+πn]
Автор ответа:
0
1) ОДЗ: 6^(x+1)-36^x>0; 6^x=t>0; 6t-t^2>0; t(t-6)<0; так как t>0⇒t-6<0; 6^x<6^1, а так как 6>1⇒x<1
Перепишем неравенство в виде: log_(1/√5)(6t-t^2)≥log_(1/√5) (1/√5)^(-2);
Так как 1/√5<1⇒6t-t^2≤5; t^2-6t+5≥0; (t-5)(t-1)≥0; t≤1 или t≥5;
в первом случае получаем 6^x≤6^0; x≤0;
во втором случае 6^x≥5; x≥log_6 5
Ответ: x∈(-∞;0]∪[log_6 5; 1)
2) Функция y=tg x монотонно возрастает на каждом интервале
(-π/2+πn;π/2+πn).
Решением соответствующего уравнения на таком интервале служит
x=π/6+πn, поэтому ответом в задаче служит объединение всех интервалов вида (-π/2+πn;π/6+πn); n∈Z
Перепишем неравенство в виде: log_(1/√5)(6t-t^2)≥log_(1/√5) (1/√5)^(-2);
Так как 1/√5<1⇒6t-t^2≤5; t^2-6t+5≥0; (t-5)(t-1)≥0; t≤1 или t≥5;
в первом случае получаем 6^x≤6^0; x≤0;
во втором случае 6^x≥5; x≥log_6 5
Ответ: x∈(-∞;0]∪[log_6 5; 1)
2) Функция y=tg x монотонно возрастает на каждом интервале
(-π/2+πn;π/2+πn).
Решением соответствующего уравнения на таком интервале служит
x=π/6+πn, поэтому ответом в задаче служит объединение всех интервалов вида (-π/2+πn;π/6+πn); n∈Z
Похожие вопросы
Предмет: Математика,
автор: ospanovagauhar03
Предмет: Математика,
автор: timuruteev1337
Предмет: Қазақ тiлi,
автор: balnurmakhan
Предмет: Алгебра,
автор: Аноним