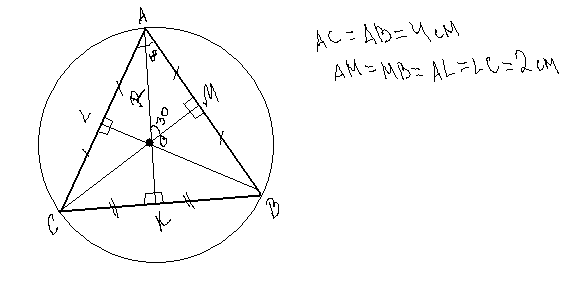
помогите пожалуйста решить! боковая сторона равнобедренного треугольника равна 4 см а угол при основании 30 градусов . найдите радиус окружности описанной около этого треугольника
Ответы
Центр описанной окружности треугольника - это точка пересечения серединных перпендикуляров. Исходя из этого можно сделать следующие вычисления:
Сначала найдем неизвестный угол равнобедренного треугольника: 180 - (30+30) = 120.
Затем проведем серединные перпендикуляры от каждой стороны треугольника и получим несколько прямоугольных треугольников, гипотенузой которых является расстояние от точки пересечения перпендикуляров до углов. Это расстояние есть радиус описанной окружности. Теперь воспользуемся чертежом. Найдем половину угла А: 120/2 = 60. Вычислим величину угла АОМ: 180 - (60+90) = 30.
Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. Катет АМ = 2см, следовательно гипотенуза, она же - радиус, равна 2*2 = 4см.
Ответ: R=4см.