Предмет: Математика,
автор: NeiroMantic
Вычислите интеграл.
Приложения:
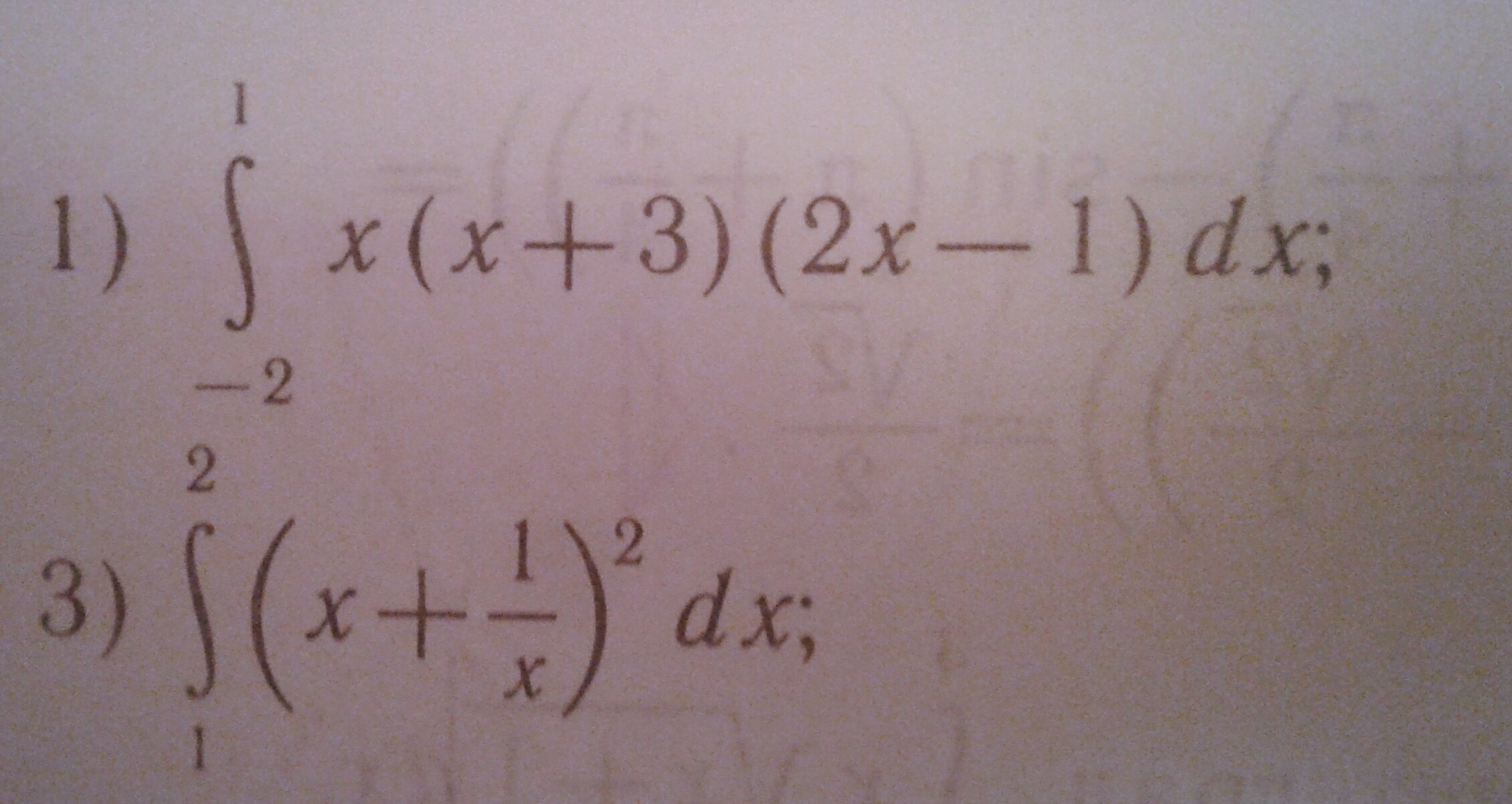
Ответы
Автор ответа:
0
1.
3.
Похожие вопросы
Предмет: География,
автор: agodkasladkaa3
Предмет: Қазақ тiлi,
автор: suleimenovakama16078
Предмет: Русский язык,
автор: golubevaelizaveta256
Предмет: Литература,
автор: smyakisheva200
Предмет: Математика,
автор: gddhih