Предмет: Алгебра,
автор: AllenWeiser1
Найдите S11 арифметич. прогрессии (An), если А6=15
Ответы
Автор ответа:
0
ответ: 165
Приложения:
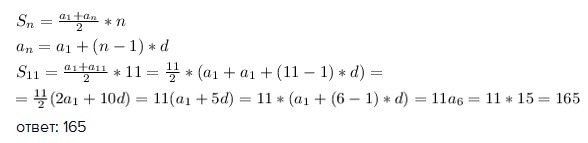
Автор ответа:
0
по свойству арифметической прогрессии

Значит:

следовательно,

Значит:
следовательно,
Приложения:
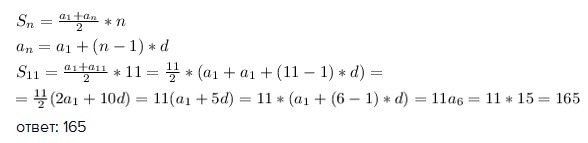
Похожие вопросы
Предмет: Английский язык,
автор: кристина071106
Предмет: Русский язык,
автор: harlampidimark
Предмет: История,
автор: kurmanovdinar2009
Предмет: Математика,
автор: binkevich
Предмет: Математика,
автор: WaterPhenix