Question

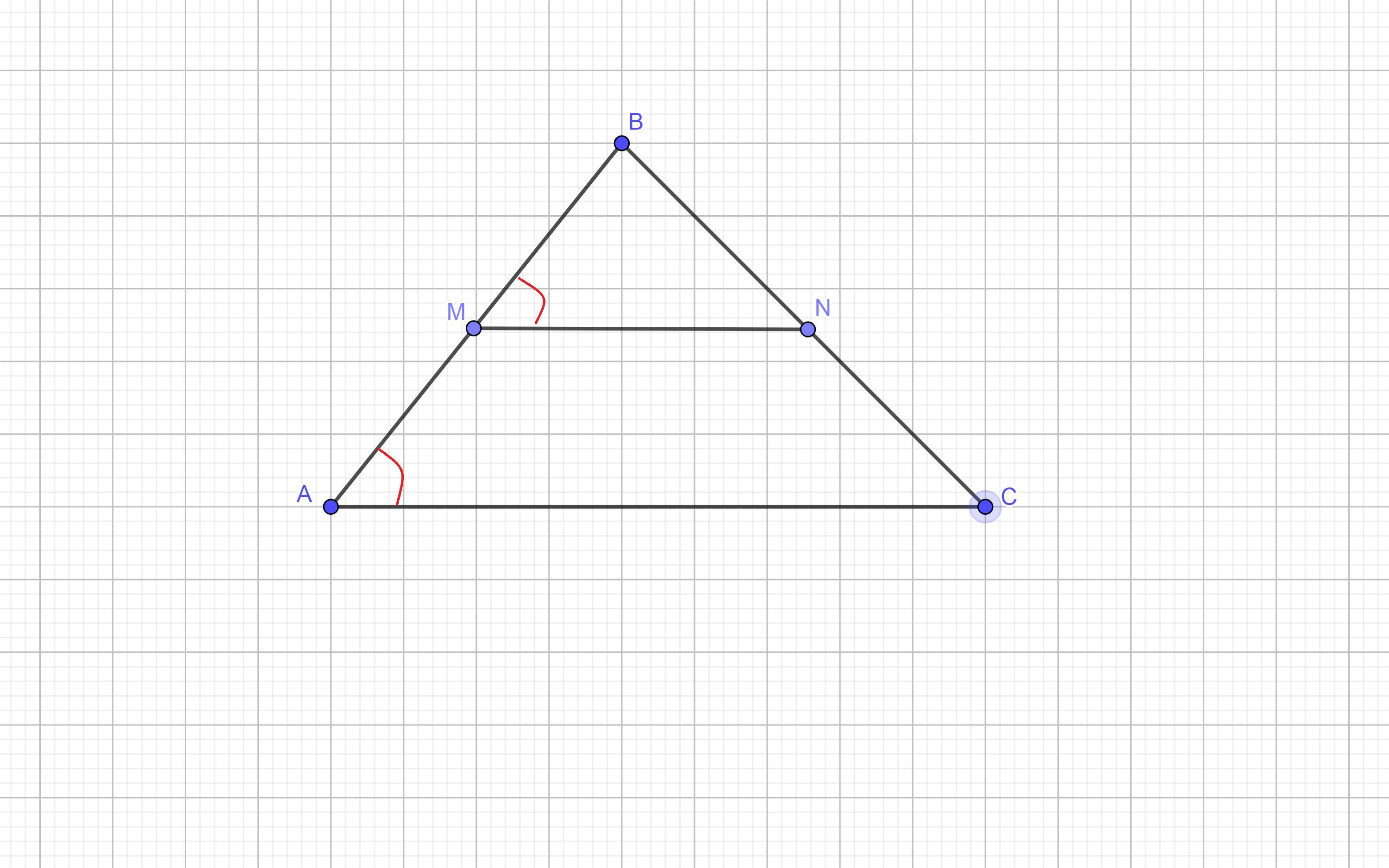
В треугольнике abc mn - средняя линия. площадь треугольника abc равна 36. найдите площадь треугольника MBN

Answer 1

Ответ:

9

Пошаговое объяснение:

Площадь ΔАВС обозначим как S1 , а площадь ΔMBN как S2

ΔАВС и ΔMBN подобны , т.к. ∠В - общий ,∠САВ=∠NMB

Отношение площадей подобных треугольников равно квадрату коэффициентов подобия.

$frac{S1}{S2}=k^{2}$

Поскольку MN - средняя линия, и она равна 1/2 основания АС, то коэффициент подобия будет

к= АС/MN= 2

По условия S1= 36  , тогда

$frac{36}{S2}= 2^{2}\ \ frac{36}{S2}=4\ \ 4S2=36\ \ S2= 36 :4\ \ S2=9$

Площадь ΔMBN  составляет 9

рисунок во вложении