Предмет: Математика,
автор: LeaDeLaria
Решите показательное уравнение и неравенство:
(5/3)^х-2=(27/125)^4+x²;
10^3x+1>0,001
Ответы
Автор ответа:
0
Приложения:
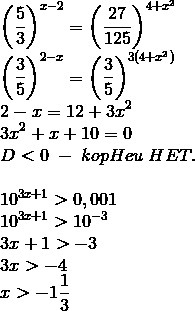
Автор ответа:
0
(5/3)^(х-2)=(3/5)^3*(4+х²)
(3/5)^(2-х)=(3/5)^(12+3х²)
2-х=12+3х²
3х²+х+12-2=0
3х²+х+10=0
Д=1²-4*3*10=1-120=-119<0
нет корней
10^(3х+1)>0,001
10^(3х+1)>10^(-3)
3х+1>-3
3х>-3-1
3х>-4
х>-4/3=-1.1/3
(3/5)^(2-х)=(3/5)^(12+3х²)
2-х=12+3х²
3х²+х+12-2=0
3х²+х+10=0
Д=1²-4*3*10=1-120=-119<0
нет корней
10^(3х+1)>0,001
10^(3х+1)>10^(-3)
3х+1>-3
3х>-3-1
3х>-4
х>-4/3=-1.1/3
Приложения:
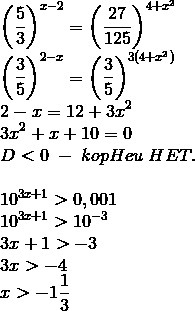
Похожие вопросы
Предмет: Математика,
автор: popovichkirill999
Предмет: Математика,
автор: alimjan11108
Предмет: Українська мова,
автор: Sashaodd
Предмет: Математика,
автор: kurbanovs457
Предмет: Математика,
автор: IngridOll