Предмет: Геометрия,
автор: Svetl121
Помогите пожалуйста правильно и грамотно решить задачу! Срочно!
Даю 50 баллов!
В равнобедренном треугольнике ABC (AB=BC) биссектрисы BD и AF пересекаются в точке O. Площадь треугольника AOB относится к площади треугольника OFD как 6:1. Найдите AC:AB.
Ответы
Автор ответа:
0
Точка О - место пересечения биссектрис треугольника АВС.
Отрезки биссектрисы, разделённые точкой пресечения биссектрис (точкой О), имеют отношение большего к меньшему как (b+c):а, где а - сторона к которой проведена биссектриса, b и с - боковые стороны угла биссектрисы.
Значит в нашем треугольнике ВО/ОД=(АВ+ВС)/АС=2АВ/АС,
АО/ОФ=(АВ+АС)/АВ.
Пусть ∠АОВ=∠ДОФ=α.
Запишем формулы нахождения площадей треугольников АОВ и OФД и сразу разделим их как показано далее по предложенному отношению:
S(ΔАОВ) = 0.5·АО·ВО·sinα
-------------------------------------- =6:1,
S(ΔOФД) = 0.5·ОД·ОФ·sinα
(ВО/ОД)·(АО/ОФ)=6,
2АВ·(АВ+АС)/(АВ·АС)=6,
2АВ+2АС=6АС,
АВ=2АС,
Итак, АС/АВ=1/2=1:2 - это ответ.
Отрезки биссектрисы, разделённые точкой пресечения биссектрис (точкой О), имеют отношение большего к меньшему как (b+c):а, где а - сторона к которой проведена биссектриса, b и с - боковые стороны угла биссектрисы.
Значит в нашем треугольнике ВО/ОД=(АВ+ВС)/АС=2АВ/АС,
АО/ОФ=(АВ+АС)/АВ.
Пусть ∠АОВ=∠ДОФ=α.
Запишем формулы нахождения площадей треугольников АОВ и OФД и сразу разделим их как показано далее по предложенному отношению:
S(ΔАОВ) = 0.5·АО·ВО·sinα
-------------------------------------- =6:1,
S(ΔOФД) = 0.5·ОД·ОФ·sinα
(ВО/ОД)·(АО/ОФ)=6,
2АВ·(АВ+АС)/(АВ·АС)=6,
2АВ+2АС=6АС,
АВ=2АС,
Итак, АС/АВ=1/2=1:2 - это ответ.
Приложения:
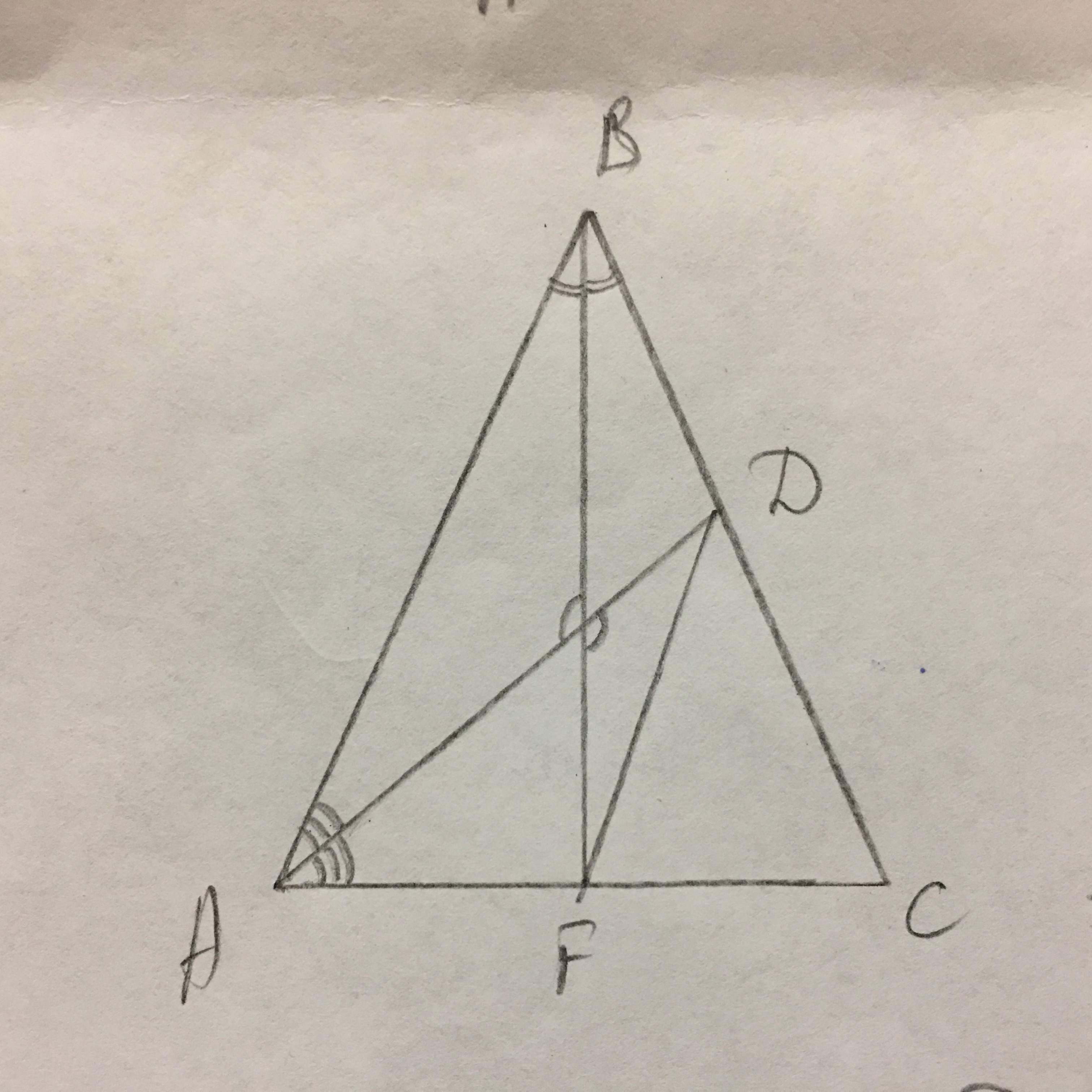
Похожие вопросы
Предмет: Окружающий мир,
автор: nelliagababyan
Предмет: Математика,
автор: karataevasajlaukul
Предмет: Английский язык,
автор: tirina260278
Предмет: Математика,
автор: AkS111
Предмет: Алгебра,
автор: AlexVPo