Предмет: Математика,
автор: Аноним
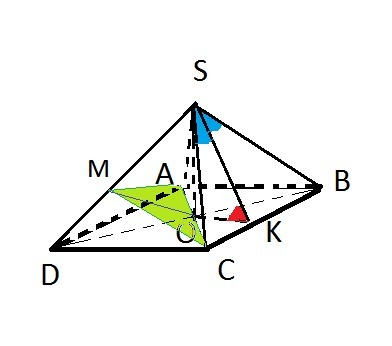
плоский угол при вершине правильной четырёхугольной пирамиды равен α.Найдите двугранные углы между плоскостью основания и боковой гранью, а также между смежными и боковыми гранями
Ответы
Автор ответа:
0
Пусть АВ=ВC=CD=AD=a
SK-биссектриса, высота и медиана равнобедренного треугольника ВSC.
Из прямоугольного треугольника
SBK
SK=a/2tg(α/2);
SB=a/2sin(α/2).
Из прямоугольного треугольника SOK
cos∠SKO=OK/SK=(a/2)/(a/2tg(α/2)) ⇒∠SKO=arccos(tg(α/2)).
Строим линейный угол двугранного угла между плоскостями
SAD и ADC.
Проводим СM⊥CD и АМ⊥СВ
∠МАС - линейный угол двугранного угла между плоскостями
SAD и ADC.
Из прямоугольного треугольника ОМА:
sin∠ОМА=ОА/МА
ОА=asqrt(2)/2
Из прямоугольного треугольника SМА
МА=SA·cosα =(acosα)/(2sin(α/2)).
sin∠ОМА=ОА/МА=(asqrt(2)/2)/(acosα)/(2sin(α/2))=sqrt(2)sin(α/2)/cosα
∠ОМА=arcsin(sqrt(2)sin(α/2)/cosα)
∠DMA=2arcsin(sqrt(2)sin(α/2)/cosα)
SK-биссектриса, высота и медиана равнобедренного треугольника ВSC.
Из прямоугольного треугольника
SBK
SK=a/2tg(α/2);
SB=a/2sin(α/2).
Из прямоугольного треугольника SOK
cos∠SKO=OK/SK=(a/2)/(a/2tg(α/2)) ⇒∠SKO=arccos(tg(α/2)).
Строим линейный угол двугранного угла между плоскостями
SAD и ADC.
Проводим СM⊥CD и АМ⊥СВ
∠МАС - линейный угол двугранного угла между плоскостями
SAD и ADC.
Из прямоугольного треугольника ОМА:
sin∠ОМА=ОА/МА
ОА=asqrt(2)/2
Из прямоугольного треугольника SМА
МА=SA·cosα =(acosα)/(2sin(α/2)).
sin∠ОМА=ОА/МА=(asqrt(2)/2)/(acosα)/(2sin(α/2))=sqrt(2)sin(α/2)/cosα
∠ОМА=arcsin(sqrt(2)sin(α/2)/cosα)
∠DMA=2arcsin(sqrt(2)sin(α/2)/cosα)
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: qwertyuiopfty80
Предмет: Геометрия,
автор: scp049pllaguedoctor
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: DinaSweet
Предмет: Алгебра,
автор: tsarevadarya0