Предмет: Алгебра,
автор: Art221122
A=3, B=1, C=4, вычислить
Приложения:
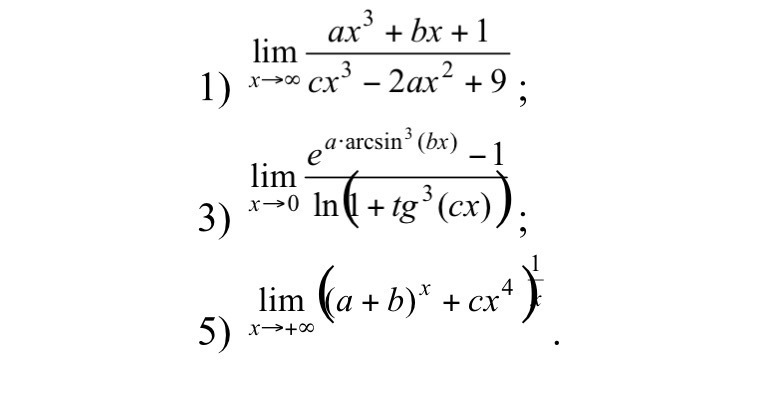
Ответы
Автор ответа:
0
Похожие вопросы