Предмет: Алгебра,
автор: Poli44444
Упростите, применив формулы сокращенного умножения:
Приложения:
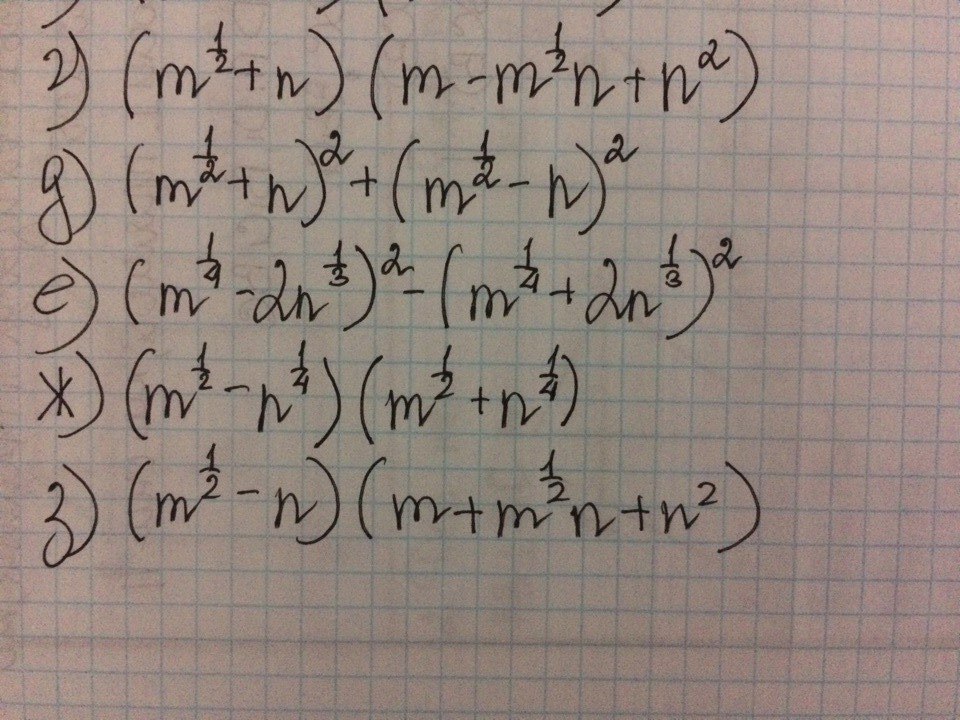
Ответы
Автор ответа:
0
Автор ответа:
0
Спасибо Огромное
Автор ответа:
0
Ответ ответ ответ ответ ответ ответ
Приложения:

Похожие вопросы
Предмет: Обществознание,
автор: adilzhan070210
Предмет: Математика,
автор: ospanovagauhar03
Предмет: Математика,
автор: bektenakmaral66
Предмет: Математика,
автор: matkadyrovaajsu