Question

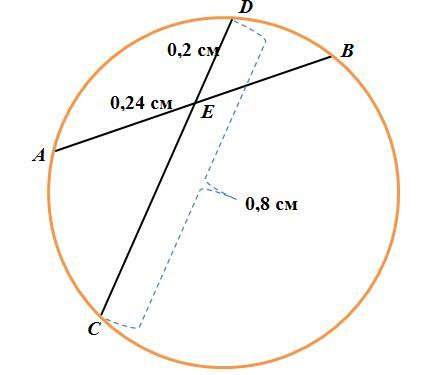
На окружности хорды AB и CD пересекаются в точке E. Найдите BE и AB, если DE=0,2 см; CD=0.8 см; AE=0,24 см.

Answer 1

Если две хорды AB и CD имеют общую точку  E. то AE*EB=CE*ED.
CE=CD-ED=0.8-0.2=0.6.Затем по свойству, написанному выше:
CE*ED=AE*EB=0.6*0.2=0.24*x
0.12=0.24x
x=0.5(BE)
AB=0.24+0.5=0.74
Ответ:0,5;0,74

Answer 2

Ответ:

BE = 0,5 см, AB = 0,74 см

Объяснение:

Из условия CD=0,8 см и DE=0,2 см. Но

EC = CD – DE= 0,8 см – 0,2 см = 0,6 см.

Отрезки пересекающихся хорд связаны соотношением AE·BE=DE·EC (см. рисунок). Подставим в равенство известные значения:

0,24 см · BE = 0,2 см · 0,6 см или

BE = 0,12 см² : 0,24 см = 0,5 см.

Тогда AB = AE + BE = 0,24 см +  0,5 см = 0,74 см.