Предмет: Алгебра,
автор: delenainTVD
Нужна помощь в решении показательного уравнения
Приложения:
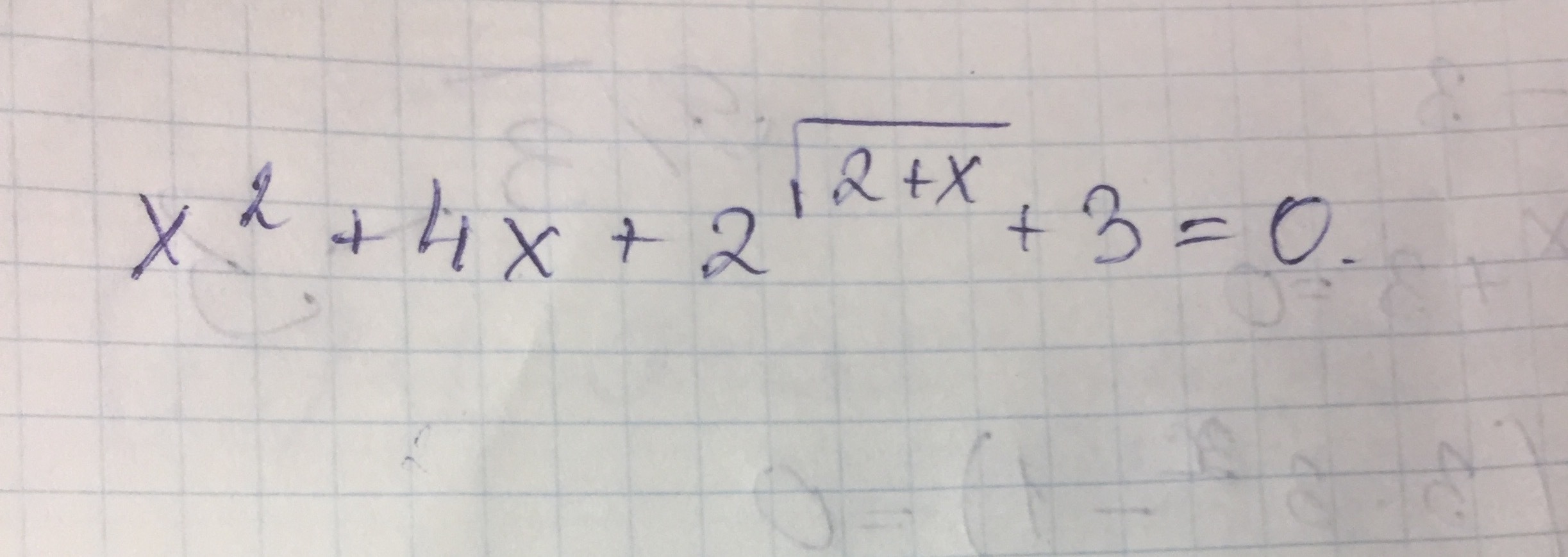
Ответы
Автор ответа:
0
1 способ решения: (свойство монотонности функций)
ОДЗ:
2+х≥0 ⇒ х≥-2

Графиком функции:

является парабола с вершиной в точке (-2;-1). Учитывая ОДЗ: x≥-2
Функция монотонно возрастает на промежутке [-2;+∞)

является монотонно убывающей функцией.
Если возрастающая функция равна убывающий, то уравнение имеет только один корень (если он есть)
Для таких задач корень находится подбором.
Если в исходном уравнении сумма чисел равна нулю, то корень (если он существует) будет отрицательный.
Нетрудно догадаться, что x=-2 (нужно было подобрать такой x, чтобы корень в показателе степени извлекся)
Ответ: -2
2 способ: (метод ограниченности функций)

так как левой частью уравнения является парабола с вершиной (-2;-1) и ветви параболы направленны вверх, то область ее значения
E(y)=[-1;+∞)
Найдем область значения правой части:

получилось так, что левая часть уравнения ≥-1, а правая≤-1
Если обе эти части равны, значит они одновременно равны -1 (в любом другом случае корней нет)

ОДЗ:
2+х≥0 ⇒ х≥-2
Графиком функции:
является парабола с вершиной в точке (-2;-1). Учитывая ОДЗ: x≥-2
Функция монотонно возрастает на промежутке [-2;+∞)
является монотонно убывающей функцией.
Если возрастающая функция равна убывающий, то уравнение имеет только один корень (если он есть)
Для таких задач корень находится подбором.
Если в исходном уравнении сумма чисел равна нулю, то корень (если он существует) будет отрицательный.
Нетрудно догадаться, что x=-2 (нужно было подобрать такой x, чтобы корень в показателе степени извлекся)
Ответ: -2
2 способ: (метод ограниченности функций)
так как левой частью уравнения является парабола с вершиной (-2;-1) и ветви параболы направленны вверх, то область ее значения
E(y)=[-1;+∞)
Найдем область значения правой части:
получилось так, что левая часть уравнения ≥-1, а правая≤-1
Если обе эти части равны, значит они одновременно равны -1 (в любом другом случае корней нет)
Похожие вопросы
Предмет: Алгебра,
автор: radmilashindav53
Предмет: Геометрия,
автор: olesiksmi
Предмет: Английский язык,
автор: bombus91
Предмет: Обществознание,
автор: sTrAIkEr830
Предмет: Математика,
автор: tatyanaminliba